K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Y
16 tháng 4 2022
\(a,\dfrac{7}{12}-\left(x+\dfrac{7}{10}\right):\dfrac{6}{5}=\dfrac{5}{4}\)
\(\Leftrightarrow\dfrac{7}{12}-x-\dfrac{7}{10}:\dfrac{6}{5}=\dfrac{5}{4}\)
\(\Leftrightarrow\dfrac{7}{12}-x-\dfrac{7}{12}=\dfrac{5}{4}\)
\(\Leftrightarrow\dfrac{7}{12}-x=\dfrac{5}{4}+\dfrac{7}{12}\)
\(\Leftrightarrow\dfrac{7}{12}-x=\dfrac{11}{6}\)
\(\Leftrightarrow x=\dfrac{7}{12}-\dfrac{11}{6}\)
\(\Leftrightarrow\dfrac{-5}{4}\)
18 tháng 8 2021
Bài 9:
a: Bạn chỉ cần vẽ tam giác ABC vuông tại A có AB=3cm và AC=4cm là ra cái hình rồi
Số đo góc A thì chắc chắn là 90 độ rồi
HM
1
1 tháng 3 2022
Bài 6:
\(B=\dfrac{1}{199}+1+\dfrac{2}{198}+1+\dfrac{3}{197}+1+...+\dfrac{198}{2}+1+1\)
\(=\dfrac{200}{199}+\dfrac{200}{198}+...+\dfrac{200}{2}+\dfrac{200}{200}\)
\(=200\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{200}\right)=200\cdot A\)
=>A/B=1/200
LB
27 tháng 3 2017
1.A= 1.2.3+2.3.4+...+29.30.31+x=15
\(4A=1.2.3.4+2.3.4.\left(5-1\right)+...+29.30.31.\left(32-28\right)+4x=60\)
\(\Rightarrow4A=1.2.3.4+2.3.4.5-1.2.3.4+...+29.30.31.32-28.29.30.31+4x=60\)
Từ đó suy ra nha bạn
2.\(\frac{2}{2.3}+\frac{2}{3.4}+...+\frac{2}{x\left(x+1\right)}=\frac{2007}{2009}\)
\(=\frac{2}{2\left(2+1\right)}+\frac{2}{3.\left(3+1\right)}+...+\frac{2}{x\left(x+1\right)}=\frac{2007}{2009}\)
\(=2.\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{x}-\frac{1}{x+1}\right)=\frac{2007}{2009}\)
\(=2.\left(\frac{1}{2}-\frac{1}{x+1}\right)=\frac{2007}{2009}\\ =1-\frac{2}{\left(x+1\right)}=\frac{2007}{2009}\)
\(\Rightarrow\frac{2}{x+1}=\frac{2}{2009}\Rightarrow x+1=2009\Rightarrow x=2008\)
AK
1
20 tháng 2 2022
Gọi số sách là x
Theo đề, ta có: \(x+2\in BC\left(10;25\right)\)
\(\Leftrightarrow x+2\in B\left(50\right)\)
mà x là số lớn nhất có 3 chữ số và thỏa mãn đề bài
nên x+2=1000
hay x=998
HH
6
A
7
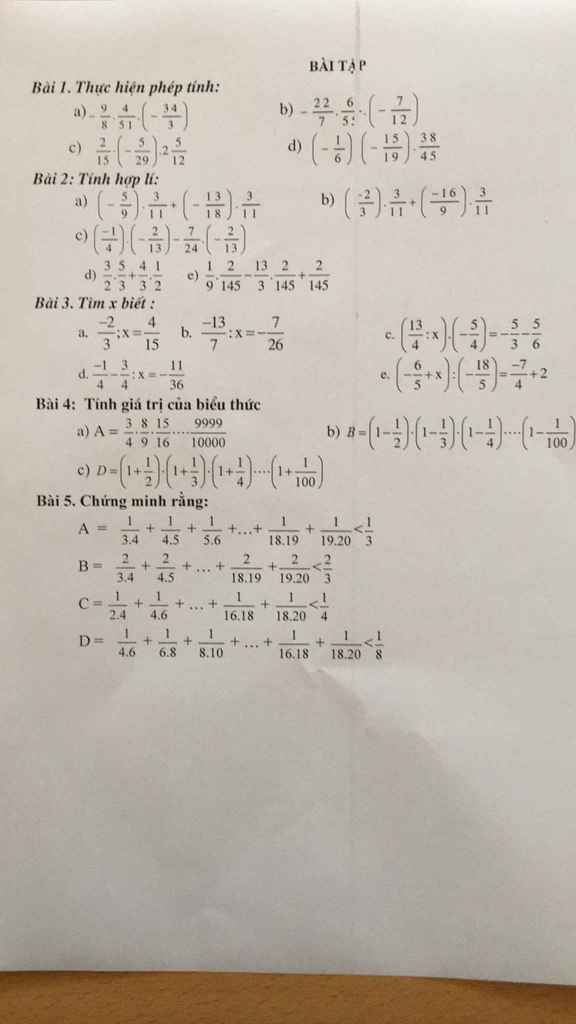
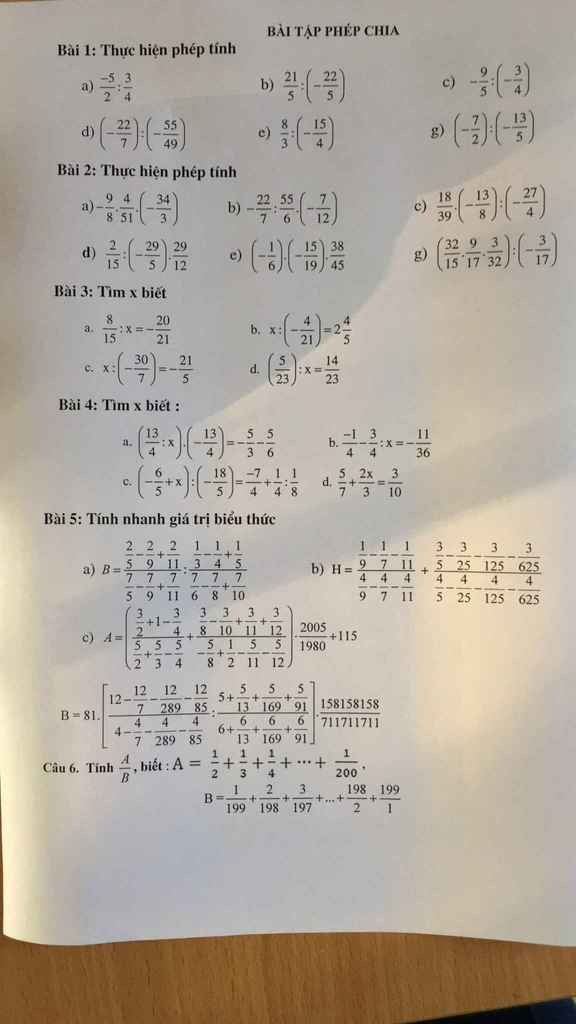
\(A=\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}=\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{20}=\dfrac{1}{3}-\dfrac{1}{20}< \dfrac{1}{3}\)
\(B=\dfrac{2}{3.4}+\dfrac{2}{4.5}+...+\dfrac{2}{19.20}=2\left(\dfrac{1}{3.4}+\dfrac{1}{4.5}+...+\dfrac{1}{19.20}\right)=2\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)=2\left(\dfrac{1}{3}-\dfrac{1}{20}\right)=\dfrac{2}{3}-\dfrac{2}{20}< \dfrac{2}{3}\)
\(C=\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{18.20}=\dfrac{1}{2}\left(\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{18.20}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+...+\dfrac{1}{18}-\dfrac{1}{20}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{20}\right)=\dfrac{1}{4}-\dfrac{1}{40}< \dfrac{1}{4}\)
\(D=\dfrac{1}{4.6}+\dfrac{1}{6.8}+...+\dfrac{1}{18.20}=\dfrac{1}{2}\left(\dfrac{2}{4.6}+\dfrac{2}{6.8}+...+\dfrac{2}{18.20}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{18}-\dfrac{1}{20}\right)=\dfrac{1}{2}\left(\dfrac{1}{4}-\dfrac{1}{20}\right)=\dfrac{1}{8}-\dfrac{1}{40}< \dfrac{1}{8}\)