
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

a: Khi x=3 thì \(A=\dfrac{3\cdot3}{3-2}=9\)
b: C=A+B
\(=\dfrac{3x}{x-2}-\dfrac{6}{x-2}-\dfrac{x^2+4x+4}{x^2-4}\)
\(=\dfrac{3x-6}{x-2}-\dfrac{x+2}{x-2}\)
\(=\dfrac{3x-6-x-2}{x-2}=\dfrac{2x-8}{x-2}\)
c: Để C nguyên thì 2x-4-4 chia hết cho x-2
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6\right\}\)

CÂU 1:
\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
CÂU 2:
\(\dfrac{12x^3y^2}{18xy^5}=\dfrac{2x^2}{3y^3}\)
CÂU 3:
\(\dfrac{15x\left(x+5\right)^3}{20x^2\left(x+5\right)}=\dfrac{3\left(x+5\right)^2}{4x}\)
CÂU 4:
\(\dfrac{3xy+x}{9y+3}=\dfrac{x\left(3y+1\right)}{3\left(3y+1\right)}=\dfrac{x}{3}\)
CÂU 5:
\(\dfrac{3xy+3x}{9y+9}=\dfrac{3x\left(y+1\right)}{9\left(y+1\right)}=\dfrac{x}{3}\)
CÂU 6:
\(\dfrac{x^2-xy}{5y^2-5xy}=\dfrac{x\left(x-y\right)}{5y\left(y-x\right)}=\dfrac{-x\left(y-x\right)}{5y\left(y-x\right)}=\dfrac{-x}{5y}\)
CÂU 7:
\(\dfrac{2x^2+2x}{x+1}=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
CÂU 8:
\(\dfrac{7x^2+14x+7}{3x^2+3x}=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\\ =\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
CÂU 9:
\(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}=\dfrac{2y}{3\left(x+y\right)^2}\)

a: BC=căn 6^2+8^2=10cm
bD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
góc B chung
=>ΔBHA đồng dạng với ΔBAC
=>BH/BA=BA/BC
=>BH*BC=BA^2
c: Xét ΔBHA có BI là phân giác
nên IH/IA=BH/BA
=>IH/IA=BA/BC=AD/DC

a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA
hay \(AB^2=HB\cdot BC\)
b: Xét ΔHAC vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\)
Do đó; ΔHAC\(\sim\)ΔHBA
SUy ra: HA/HB=HC/HA
hay \(HA^2=HB\cdot HC\)
a) Xét ∆ABC(<A=90 ° ) và ∆HBA(<H=90 ° ), ta có:
<B chung ⟹∆ABC~ ∆HBA(g.g)
⟹AB/HB=BC/AB⟹AB*AB=HB*BC hay AB2=BH*BC
b)Xét ∆HAC(<H=90 °) và ∆HBA(<H=90 ° ), ta được:
<B=<HAC( vì cùng phụ với <BAH do <B+<BAH =90°; <HAC+<BAH =90°)
⟹∆HAC~∆HBA(g.g)
⟹HA/HB=HC/HA⟹HA*HA=HB*HC hayHA2=BH*CH

Bài 6:
a: Xét ΔABC có
D là trung điểm của BC
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//AB và \(DM=\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)

a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC
hay DECB là hình thang


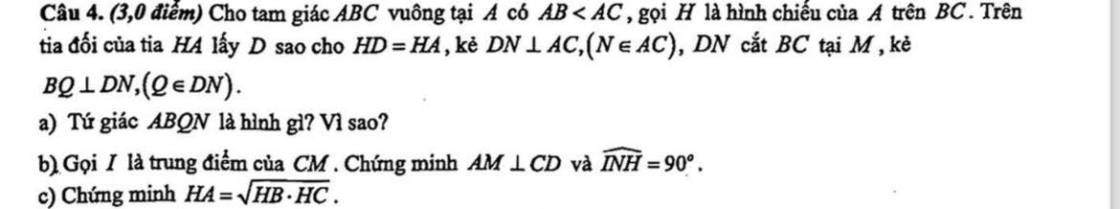
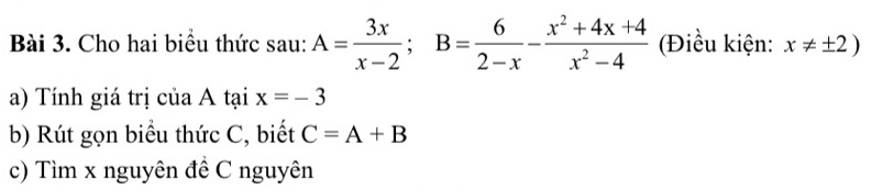








do từ câu b ta có MHNK là hình vuông từ đó ta có
MN là trung trực của KH (1)
mà ta có hai tam giác vuông IKB và IHB nên ta có \(PH=PK=\frac{1}{2}BI\)( đường trung tuyến ứng với cạnh huyền)
Do PH=PK nên P thuộc đường trung trực của KH (2)
từ (1) và (2) ta có P thuộc MN
chứng minh tương tự ta có
Q thuộc MN
do đó M,N,P,Q thẳng hàng