
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3: \(\left(\dfrac{1}{\sqrt{2}-1}-\dfrac{1}{\sqrt{2}+1}\right):\sqrt{3-2\sqrt{2}}\)
\(=\dfrac{\sqrt{2}+1-\sqrt{2}+1}{2-1}:\left(\sqrt{2}-1\right)\)
\(=\dfrac{2}{\sqrt{2}-1}=2\left(\sqrt{2}+1\right)=2\sqrt{2}+2\)
5:
\(\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}+\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}\)
\(=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2+\left(\sqrt{5}-\sqrt{3}\right)^2}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}\)
\(=\dfrac{8+2\sqrt{15}+8-2\sqrt{15}}{2}=\dfrac{16}{2}=8\)
6:
\(\dfrac{\sqrt{5}-1}{\sqrt{5}+1}-\dfrac{\sqrt{5}+1}{\sqrt{5}-1}\)
\(=\dfrac{\left(\sqrt{5}-1\right)^2-\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{6-2\sqrt{5}-6-2\sqrt{5}}{4}=\dfrac{-4\sqrt{5}}{4}=-\sqrt{5}\)
4:
\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{2}-\sqrt{3}+3\right)}\)
\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{5-2\sqrt{6}-9}=\dfrac{-6\left(\sqrt{2}-\sqrt{3}-3\right)}{4+2\sqrt{6}}\)
\(=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)}{\sqrt{6}+2}=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)\left(\sqrt{6}-2\right)}{2}\)
\(=\dfrac{-3\left(2\sqrt{3}-2\sqrt{2}-3\sqrt{2}+2\sqrt{3}-6\sqrt{3}+6\right)}{2}\)
\(=\dfrac{-3\left(-2\sqrt{3}-5\sqrt{2}+6\right)}{2}\)

a, Vì ME là tiếp tuyến đường tròn O và M là tiếp điểm
=> \(MO\perp MF\) ( t/c tiếp tuyến ) hay ^OME = 900
Vậy tam giác EMO là tam giác vuông tại M
b, mình sửa đề là OE = 60 cm nhé
Theo định lí Pytago cho tam giác EMO vuông tại M
\(ME=\sqrt{EO^2-OM^2}=48\)cm
c, sửa ON vuông OE tại N
đến đây thì mình chả hiểu đề kiểu gì, chịu, bạn chép đề kiểu gì ấy, sai tào lao sao á, xem lại nhé
a: Xét ΔMEO có \(\widehat{OME}=90^0\)
nên ΔMEO vuông tại M

a) Xét \(\left(O\right):\)
+) Ta có: Dây AB = Dây AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow\stackrel\frown{AB}=\stackrel\frown{AC}.\)
+) \(\widehat{ABM}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
Mà \(\stackrel\frown{AB}=\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\widehat{ABM}=\widehat{ABC}.\)
\(\Rightarrow\) BA là phân giác \(\widehat{CBM}.\)
b) Xét \(\left(O\right):\)
\(\widehat{MBA}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc tạo bởi tia tiếp tuyến và dây cung).
\(\widehat{MDB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\) (Góc nội tiếp).
\(\Rightarrow\widehat{MBA}=\widehat{MDB}.\)
Xét \(\Delta MAB\) và \(\Delta MBD:\)
\(\widehat{MBA}=\widehat{MDB}.\)
\(\widehat{BMD}chung.\)
\(\Rightarrow\Delta MAB\sim\Delta MBD\left(g-g\right).\)
\(\Rightarrow\dfrac{MA}{MB}=\dfrac{MB}{MD}\) (Cặp cạnh tương ứng tỉ lệ).
\(\Rightarrow MA.MD=MB^2.\)

Bài 3:
a:Ta có: \(\sqrt{4x^2-4x+1}=3\)
\(\Leftrightarrow\left|2x-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b: Ta có: \(2\sqrt{x-1}-4=0\)
\(\Leftrightarrow x-1=4\)
hay x=5



1) \(\sqrt{2-\sqrt{3}}\left(\sqrt{5}+\sqrt{2}\right)=\sqrt{\dfrac{4-2\sqrt{3}}{2}}\left(\sqrt{5}+\sqrt{2}\right)\)
\(=\sqrt{\dfrac{\left(\sqrt{3}-1\right)^2}{2}}\left(\sqrt{5}+\sqrt{2}\right)=\dfrac{\sqrt{3}-1}{\sqrt{2}}\left(\sqrt{5}+\sqrt{2}\right)=\dfrac{\sqrt{15}+\sqrt{6}-\sqrt{5}-\sqrt{2}}{\sqrt{2}}\)
theo mình nghĩ thì đề nên là \(\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\)
như thế thì sẽ \(=\dfrac{\sqrt{3}-1}{\sqrt{2}}.\sqrt{2}\left(\sqrt{3}+1\right)=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)=2\) đẹp hơn,đó là mình nghĩ vậy thôi,còn nếu đề bạn đúng thì mình làm ở trên đó
2) \(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}=\sqrt{\dfrac{6-2\sqrt{5}}{2}}+\sqrt{\dfrac{6+2\sqrt{5}}{2}}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-1\right)^2}{2}}+\sqrt{\dfrac{\left(\sqrt{5}+1\right)^2}{2}}=\dfrac{\sqrt{5}-1}{\sqrt{2}}+\dfrac{\sqrt{5}+1}{\sqrt{2}}=\dfrac{2\sqrt{5}}{\sqrt{2}}=\sqrt{10}\)
3) Đặt \(A=\sqrt{4+\sqrt{10+2\sqrt{5}}}+\sqrt{4-\sqrt{10+2\sqrt{5}}}\)
\(\Rightarrow A^2=8+2\sqrt{\left(4+\sqrt{10+2\sqrt{5}}\right)\left(4-\sqrt{10+2\sqrt{5}}\right)}\)
\(=8+2\sqrt{16-\left(10+2\sqrt{5}\right)}=8+2\sqrt{6-2\sqrt{5}}\)
\(=8+2\sqrt{\left(\sqrt{5}-1\right)^2}=8+2\sqrt{5}-2=6+2\sqrt{5}=\left(\sqrt{5}+1\right)^2\)
\(\Rightarrow A=\sqrt{5}+1\left(A\ge0\right)\)
4) \(\dfrac{\left(\sqrt{5}+2\right)^2-8\sqrt{5}}{2\sqrt{5}-4}=\dfrac{9+4\sqrt{5}-8\sqrt{5}}{2\left(\sqrt{5}-2\right)}=\dfrac{9-4\sqrt{5}}{2\left(\sqrt{5}-2\right)}\)
\(=\dfrac{\left(\sqrt{5}-2\right)^2}{2\left(\sqrt{5}-2\right)}=\dfrac{1}{2}\)

1
Có: \(tgB=\dfrac{CA}{CB}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)
\(cotgB=\dfrac{CB}{CA}=\dfrac{1,2}{0,9}=\dfrac{4}{3}\)
Vì A, B phụ nhau nên:
\(cotgA=tgB=\dfrac{3}{4}\\ tgA=cotgB=\dfrac{4}{3}\)
Áp dụng pytago vào tam giác ABC vuông tại C, có:
\(AB^2=BC^2+AC^2=1,2^2+0,9^2=1,5^2\Rightarrow AB=1,5\left(vì.AB>0\right)\)
Do đó: \(sinB=\dfrac{CA}{AB}=\dfrac{0,9}{1,5}=\dfrac{3}{5};cosB=\dfrac{CB}{BA}=\dfrac{1,2}{1,5}=\dfrac{4}{5}\)
Vì A, B phụ nhau nên:
\(sinA=cosB=\dfrac{4}{5};cosA=sinB=\dfrac{3}{5}\)
3:
a: Xét ΔBAC có AB^2=CA^2+CB^2
nên ΔABC vuông tại C
b: sin A=cos B=BC/AC=căn 15/5
cos A=sin A=CA/BC=căn 2/5=1/5*căn 10
tan A=cot B=căn 15/căn 10=căn 3/2
cot A=tan B=căn 2/3
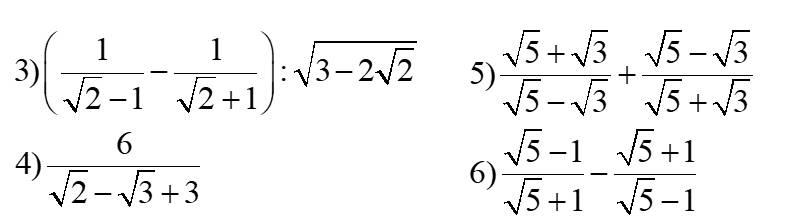


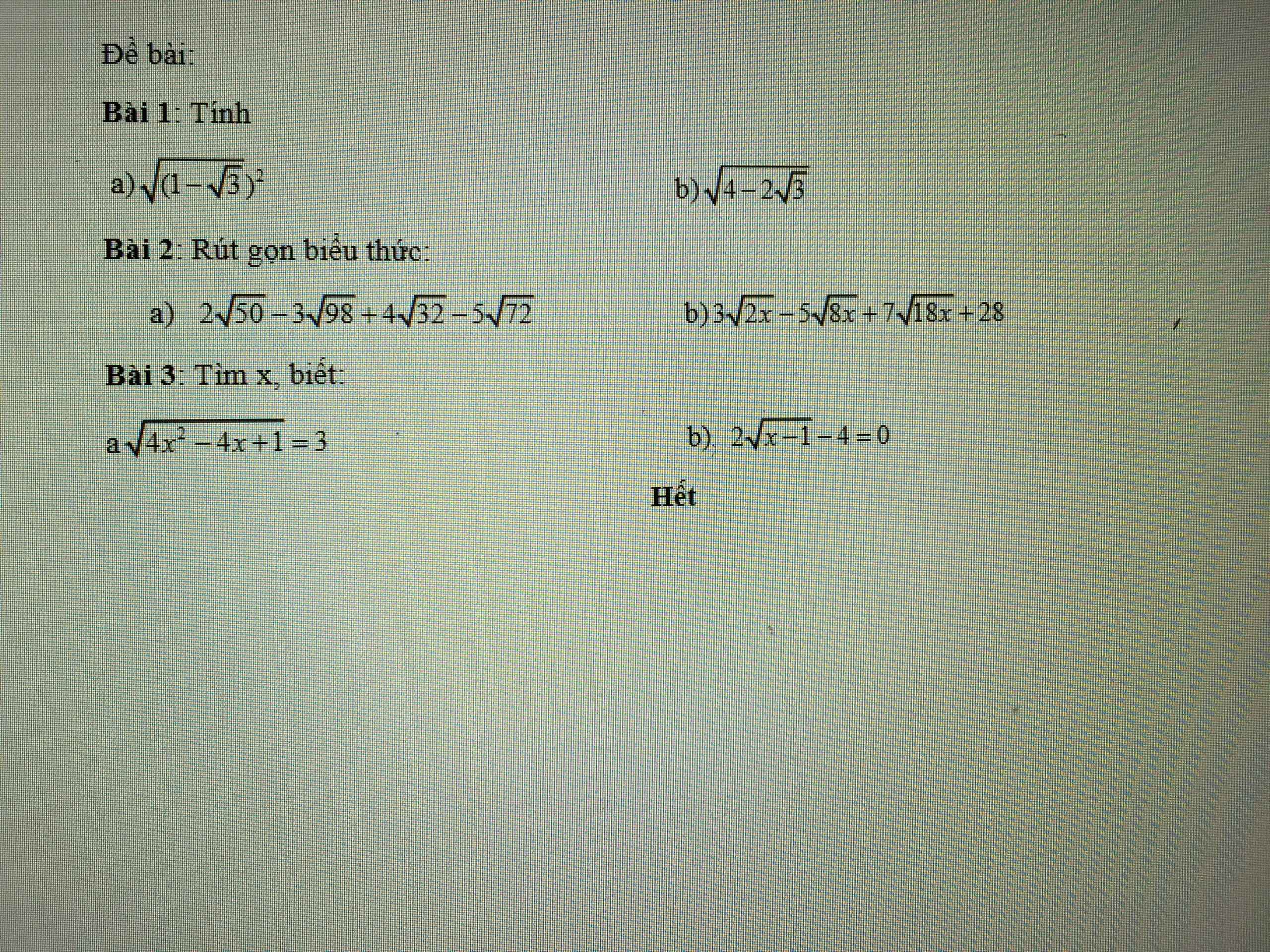 Giúp mình vs ạ. Cảm ơn trước ạ!
Giúp mình vs ạ. Cảm ơn trước ạ!

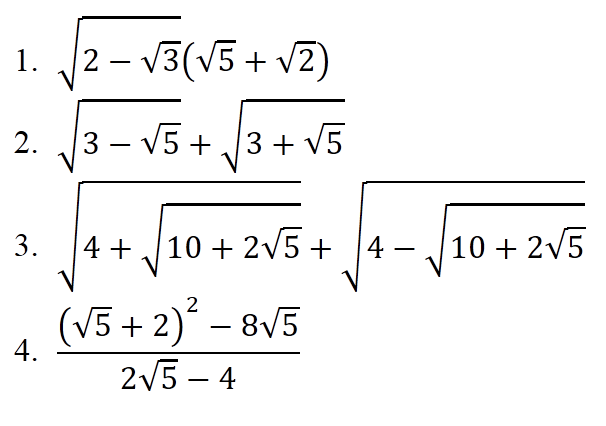

a. PTHDGD: \(\dfrac{2}{5}x-\dfrac{4}{3}=x+2\Leftrightarrow\dfrac{3}{5}x=-\dfrac{10}{3}\Leftrightarrow x=-\dfrac{50}{9}\Leftrightarrow y=-\dfrac{32}{9}\Leftrightarrow A\left(-\dfrac{50}{9};-\dfrac{32}{9}\right)\)
Vậy \(A\left(-\dfrac{50}{9};-\dfrac{32}{9}\right)\) là tọa độ giao điểm
b. PTHDGD: \(x-2=3x+4\Leftrightarrow x=-3\Leftrightarrow y=-5\Leftrightarrow B\left(-3;-5\right)\)
Vậy \(B\left(-3;-5\right)\) là tọa độ giao điểm