Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B

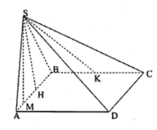
Ta có B C ⊥ S M . Gọi H là hình chiếu vuông góc của A trên SM. Do
![]() và FE đi qua H.
và FE đi qua H.
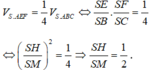
Vậy H là trung điểm cạnh SM. Suy ra tam giác SAM vuông cân tại A
⇒ S A = a 3 2 V S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8
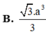
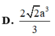

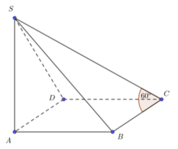

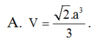
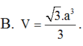
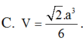
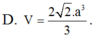
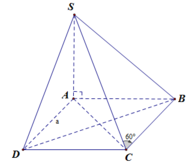

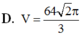

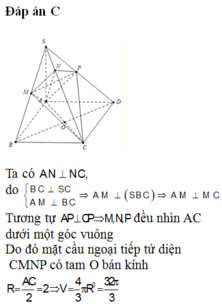
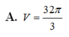
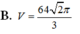
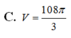
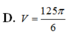


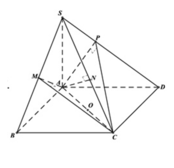
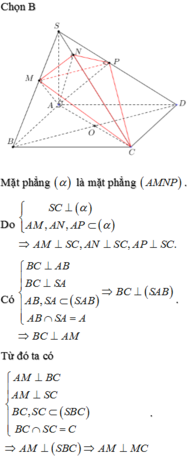


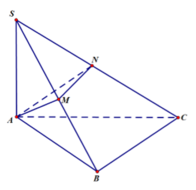
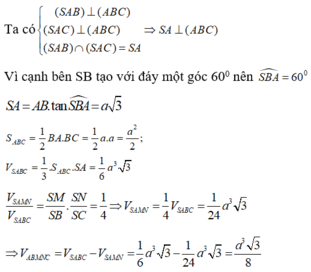

ta có (SBD) giao với (ABCD) theo gt BD
BD vuông AC và BD vuong SA nên BD vuông (SAC)
góc đó là góc SOA
xét tam giác vuông SAO có tan 60*=SA/ÁO mà AC= a căn 2 nên ÁO=a căn 2 trên 2
=>SA=a căn 6 trên 2
xét VSABCD =SB.SC =1/2.1/2=1/4 (M,N là trung diểm)
VSAMND SM.SN
MÀ VSABCD=1/3.SA.SABCD=1/3.a căn 6/2.a^2=a^3 căn 6/6
=>VSAMND=1/4.VSABCD=a căn 6/24