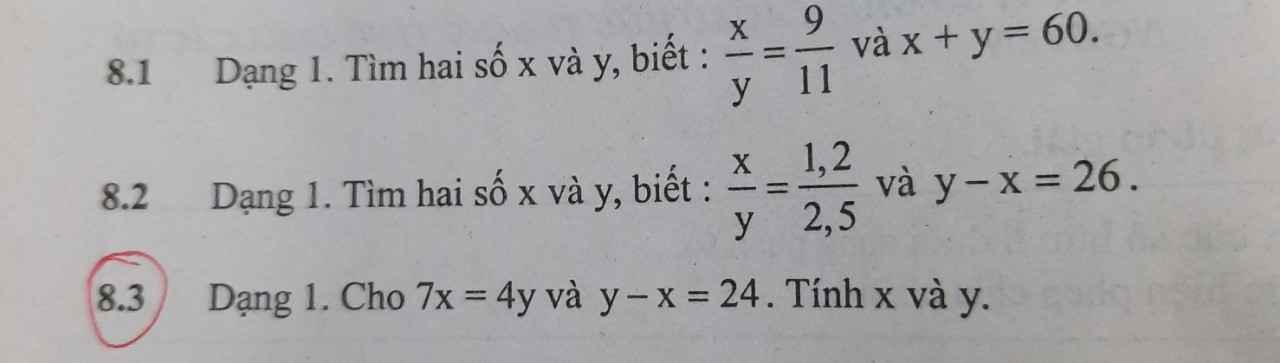K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 8 2018
Gọi giao điểm của AH và DC là I.
AF song song với DI (cùng vuông góc với AD) (1)
\(\Delta ADI=\Delta BAE\left(g.c.g\right)\Rightarrow DI=AE\) ( 2 cạnh tương ứng )
Mà \(AE=AF\left(gt\right)\Rightarrow DI=AF\) (2)
Từ (1) và (2) \(\Rightarrow AFID\)là hình bình hành.
Mà \(\widehat{FAD}=90^0\Rightarrow AFID\) là hình chữ nhật.
Từ đó: FBCI là hình chữ nhật nên IB = CF (t/c hình chữ nhật)
Gọi O là giao điểm của FC và BI \(\Rightarrow O\) là trung điểm của FC và BI
\(\Delta BHI\) vuông tại B có HO là đường trung tuyến ứng với cạnh CF nên
\(HO=\frac{1}{2}BI\Rightarrow HO=\frac{1}{2}CF\)
\(\Delta CHF\)có đường trung tuyến HO = 1/2 CF nên \(\Delta CHF\) vuông tại H.
Vậy \(\widehat{CHF}=90^0\)
Mình chỉ hướng dẫn bước thôi. Bạn tự trình bày nhé
Mong bạn hiểu lời giải. Chúc bạn học tốt.
27 tháng 12 2018
Bài này hơi dài, c tham khảo ở đây nè https://cunghocvui.com/danh-muc/toan-lop-8
AH
Akai Haruma
Giáo viên
16 tháng 10 2021
8.3
$7x=4y\Rightarrow x=\frac{4}{7}y$. Khi đó:
$y-x=24$
$y-\frac{4}{7}y=24$
$\frac{3}{7}y=24$
$y=56$
$x=\frac{4}{7}y=\frac{4}{7}.56=32$
LT
2
24 tháng 7 2016
\(2x^2-x-15\)
\(2x^2-x-15\)
\(=\left(x-3\right)\left(x+\frac{5}{2}\right)\)
28 tháng 2 2016
(x - 6) = (84 - x ) + 6
x - 6 = 84 - x + 6
-x - x = -6 - 84 - 6
-2x = -96
Vậy x = (-96) : (-2) = 48
LT
3
Y
4 tháng 8 2016
1-x-2x^2
= 1-x-2x.2x
= 1 - ( x + 2x.2x)
= 1 - 5x
Để 1-x-2x^2 mang giá trị lớn nhất thì x phài là số âm.
OP
4 tháng 8 2016
\(A=1-x-2x^2\)
\(=-2\left(x^2+2\times x\times\frac{1}{4}+\left(\frac{1}{4}\right)^2-\left(\frac{1}{4}\right)^2-\frac{1}{2}\right)\)
\(=-2\left[\left(x+\frac{1}{4}\right)^2-\frac{9}{16}\right]\)
\(\left(x+\frac{1}{4}\right)^2\ge0\)
\(\left(x+\frac{1}{4}\right)^2-\frac{9}{16}\ge-\frac{9}{16}\)
\(-2\left[\left(x+\frac{1}{4}\right)^2-\frac{9}{16}\right]\le\frac{9}{8}\)
Vậy Max A = \(\frac{9}{8}\) khi x = \(-\frac{1}{4}\)