
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


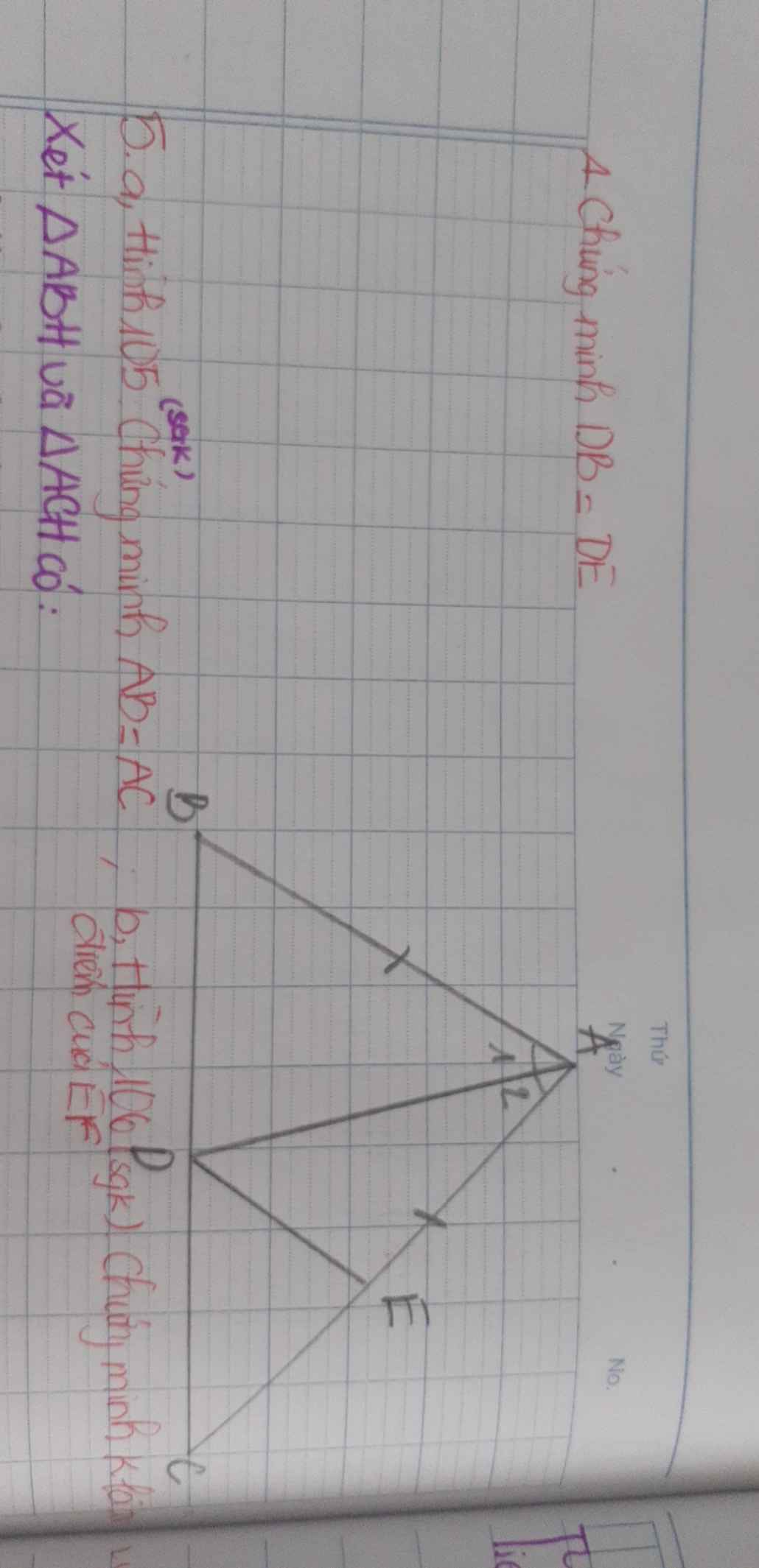
4) Xét \(\Delta ADB\) và \(\Delta ADE\) có:
AB=AE
\(\widehat{A_1}=\widehat{A_2}\)
AD chung
Vậy \(\Delta ADB=\Delta ADE\left(c.g.c\right)\)
\(\Rightarrow DB=DE\left(2.cạnh.tương.ứng\right)\)

a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAI vuông tại A và ΔBHI vuông tại H có
BI chung
góc ABI=góc HBI
=>ΔBAI=ΔBHI
=>IA=IH
mà IH<IC
nên IA<IC
c: Xét ΔIAK vuông tại A và ΔIHC vuông tại H có
IA=IH
góc AIK=góc HIC
=>ΔIAK=ΔIHC
=>AK=HC
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC


Ta có: \(\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}-\dfrac{1}{x}=-\dfrac{1}{2011}\)
\(\Leftrightarrow\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}-\dfrac{1}{x}=-\dfrac{1}{2011}\)
\(\Leftrightarrow x+4=8044\)
hay x=8040

\(Q=\left|x-1\right|+\left|3-x\right|+\left|x-2\right|\)
\(Q\ge\left|x-1+3-x\right|+\left|x-2\right|=2+\left|x-2\right|\ge2\)
Vậy \(Q_{min}=2\) khi \(x=2\)

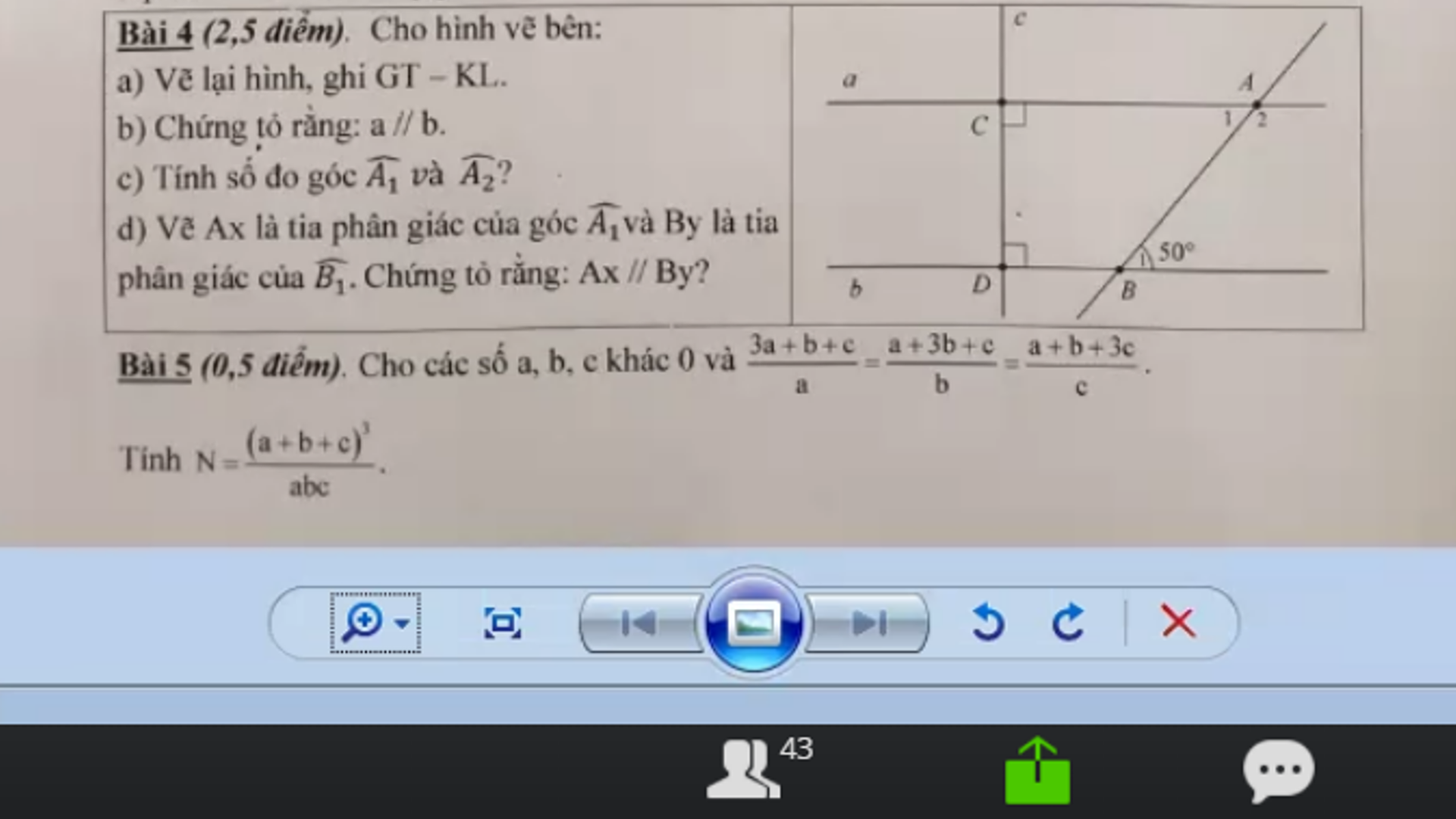
c) \(\widehat{A1}=\widehat{B1}\)(là 2 góc so le trong)
Mà \(\widehat{B1}=50độ\)
\(\Rightarrow\)\(\widehat{A1}=50độ\)
Vì \(\widehat{A1}+\widehat{A2}=180độ\)(2 góc kề bù)
Hay 50độ + \(\widehat{A2}\) = 180 độ
\(\widehat{A2}\) = 180độ - 50độ
\(\widehat{A2}\) = 130độ
Vậy \(\widehat{A1}=50độ\)
\(\widehat{A2}\) = 130độ


\(\widehat{E_1}=\widehat{C_7}=60^o\)(hai góc so le trong do d'//d")
\(\widehat{G_2}=\widehat{D_3}=110^o\)(hai góc đồng vị do d'//d")
\(\widehat{G_3}=180^o-\widehat{G_2}=180^o-110^o=70^o\)(hai góc kề bù)
\(\widehat{D_4}=\widehat{D_3}=110^o\)(hai góc đối đỉnh)
\(\widehat{A_5}=\widehat{E_1}=60^o\)(hai góc đồng vị do d//d")
\(\widehat{B_6}=\widehat{G_3}=70^o\)(hai góc đồng vị do d//d")
https://hoc24.vn/cau-hoi/giup-minh-voi-minh-dang-can-gap.4764607487635
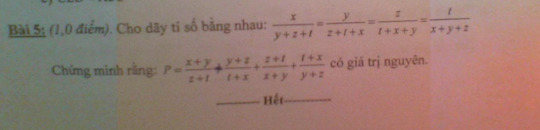





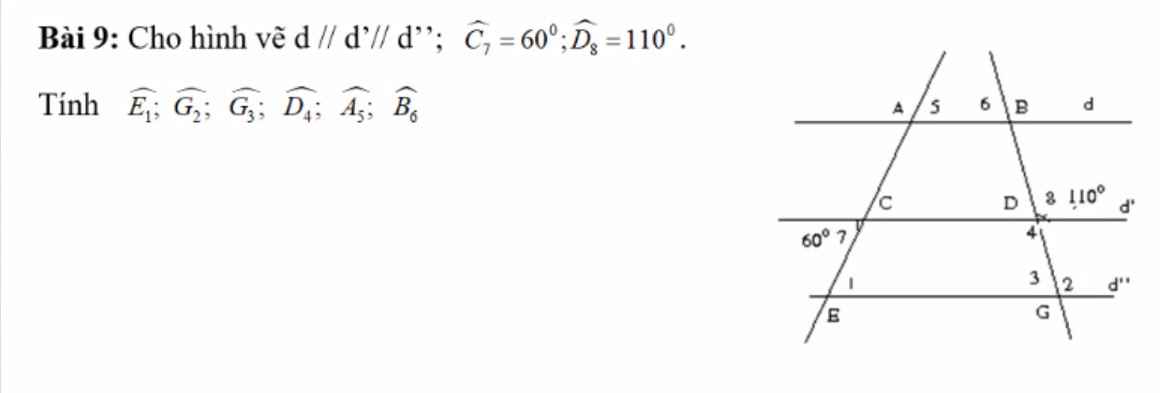
TH1: \(x+y+z+t\ne0\)
Áp dụng t/c dtsbn ta có:
\(\dfrac{x}{y+z+t}=\dfrac{y}{z+t+x}=\dfrac{z}{t+x+y}=\dfrac{t}{x+y+z}=\dfrac{x+y+z+t}{3\left(x+y+z+t\right)}=\dfrac{1}{3}\)\(\dfrac{x}{y+z+t}=\dfrac{1}{3}\Rightarrow3x=y+z+t\Rightarrow4x=x+y+z+t\\ \dfrac{y}{z+t+x}=\dfrac{1}{3}\Rightarrow3y=x+z+t\Rightarrow4y=x+y+z+t\\ \dfrac{z}{t+x+y}=\dfrac{1}{3}\Rightarrow3z=x+y+t\Rightarrow4z=x+y+z+t\\ \dfrac{t}{x+y+z}=\dfrac{1}{3}\Rightarrow3t=x+y+z\Rightarrow4t=x+y+z+t\)
\(\Rightarrow4x=4y=4z=4t\\ \Rightarrow x=y=z=t\)
\(P=\dfrac{x+y}{z+t}+\dfrac{y+z}{t+x}+\dfrac{z+t}{x+y}+\dfrac{t+x}{y+z}\\ =1+1+1+1\\ =4\)
TH2: \(x+y+z+t=0\)
\(\Rightarrow\left\{{}\begin{matrix}x+y=-\left(z+t\right)\\y+z=-\left(x+t\right)\\z+t=-\left(x+y\right)\\t+x=-\left(y+z\right)\end{matrix}\right.\)
\(P=\dfrac{x+y}{z+t}+\dfrac{y+z}{t+x}+\dfrac{z+t}{x+y}+\dfrac{t+x}{y+z}\\ =\dfrac{-\left(z+t\right)}{z+t}+\dfrac{-\left(t+x\right)}{t+x}+\dfrac{-\left(x+y\right)}{x+y}+\dfrac{-\left(y+z\right)}{y+z}\\ =-1-1-1-1\\ =-4\)
nghĩa là sao viết tắt quá