
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Khi x<0 thì hàm số đồng biến
b: PTHĐGĐ là:
-x^2=2x-3
=>-x^2-2x+3=0
=>x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=1 hoặc x=-3
=>y=-1 hoặc y=-9
c: Thay y=-4vào (P),ta được:
x^2=4
=>x=2 hoặc x=-2


Lời giải:
a. Số tiền phạt cho $20$ kg hành lý quá cước là:
$T=\frac{4}{5}.20+20=36$ (USD)
b.
$651980$ VNĐ = $\frac{651980}{23285}=28$ USD
Ta có: $28=\frac{4}{5}M+20$
$8=\frac{4}{5}M$
$M=10$ (kg)
Vậy khối lượng hành lý quá cước là $10$ kg.

c: Phương trình hoành độ giao điểm của \(\left(d1\right),\left(d2\right)\) là:
x-2=3x-4
\(\Leftrightarrow x-3x=-4+2\)
\(\Leftrightarrow-2x=-2\)
hay x=1
Thay x=1 vào y=x-2, ta được:
y=1-2=-1
Thay x=1 và y=-1 vào \(\left(d\right)\), ta được:
\(m^2-3m+1+m-1=-1\)
\(\Leftrightarrow m^2-2m+1=0\)
\(\Leftrightarrow m-1=0\)
hay m=1


`a)m=0=>x^2-x+3=0<=>(x-1/2)^2+11/4=0` (Vô lí)
`=>m=0` ptr vô nghiệm
`b)` Ptr có nghiệm kép `<=>\Delta=0`
`<=>[-(2m+1)]^2-4(m^2+3)=0`
`<=>4m^2+4m+1-4m^2-12=0`
`<=>4m-11=0`
`<=>m=11/4`
`c)` Ptr có `2` nghiệm pb`<=>\Delta > 0`
`<=>4m-11 > 0<=>m > 11/4`
`d)` Ptr vô nghiệm `<=>\Delta < 0<=>4m-11 < 0<=>m < 11/4`
Bài 2:
a: Khi m=0 thì pt sẽ là:
\(x^2-x+3=0\)
=>\(x\in\varnothing\)
b: \(\Delta=\left(2m+1\right)^2-4\left(m^2+3\right)\)
=4m^2+4m+1-4m^2-12
=4m-11
Để pt có nghiệm kép thì 4m-11=0
=>m=11/4
c: Để phương trình có hai nghiệm pb thì 4m-11>0
=>m>11/4
d: Để pt vô nghiệm thì 4m-11<0
=>m<11/4

Bài 1:
Xét tứ giác ABDC có \(\widehat{A}+\widehat{D}=180^0\)
nên ABDC là tứ giác nội tiếp

Bài 2:
a: Để hai đồ thị song song thì 2m-1=m+2
hay m=3
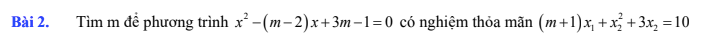








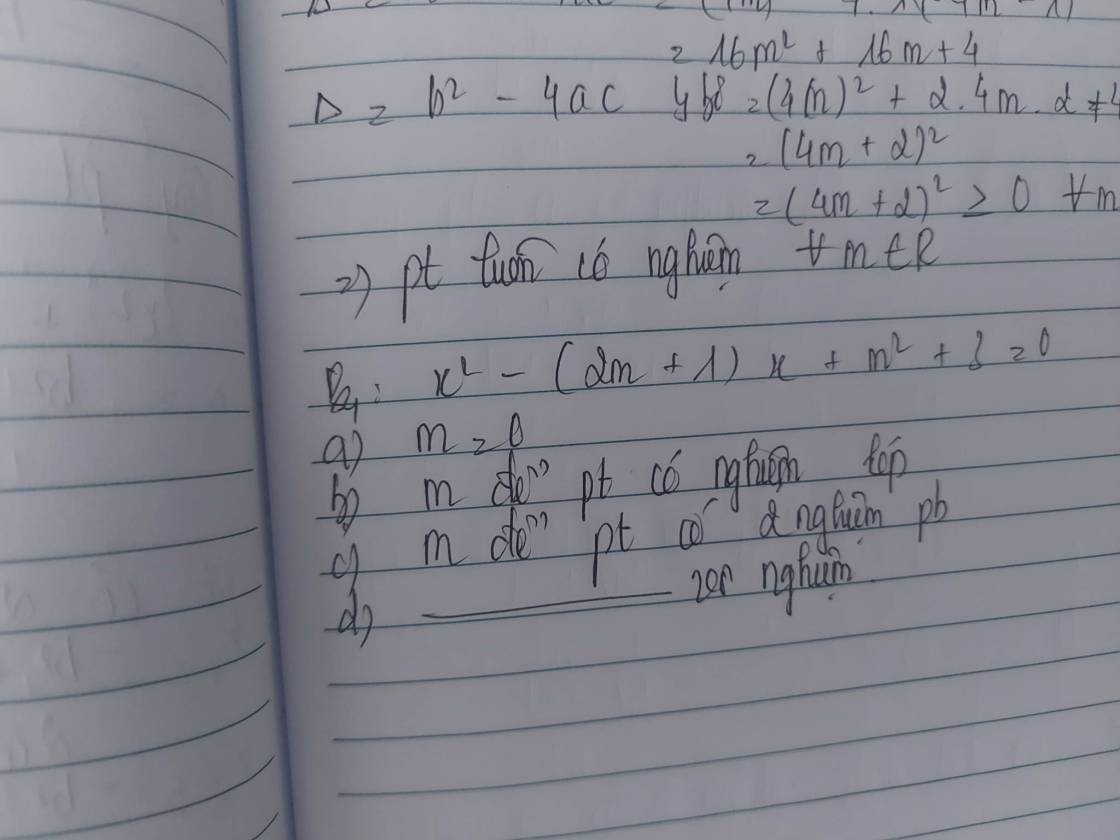

 giúp mình với ạ mình cảm ơn nhiều
giúp mình với ạ mình cảm ơn nhiều 
Bài 2.
\(x^2-\left(m-2\right)x+3m-1=0\)
\(\Delta=\left(m-2\right)^2-4\left(3m-1\right)=m^2-16m+8\)
PT có hai nghiệm \(x_1,x_2\)\(\Leftrightarrow\Delta\ge0\Leftrightarrow m^2-16m+8\ge0\)
Khi đó, áp dụng hệ thức Vi - et ta có: \(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=3m-1\end{matrix}\right.\)
Để \(\left(m+1\right)x_1+x_2^2+3x_2=10\Leftrightarrow\left(m-2\right)x_1+3x_1+x_2^2+3x_2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)x_1+x_2^2+3\left(x_1+x_2\right)=10\)
\(\Leftrightarrow x_1^2+x_2^2+x_1x_2+3\left(x_1+x_2\right)=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-x_1x_2+3\left(x_1+x_2\right)=10\)
\(\Leftrightarrow\left(m-2\right)^2-\left(3m-1\right)+3\left(m-2\right)=10\)
\(\Leftrightarrow m^2-4m-11=0\Leftrightarrow\left[{}\begin{matrix}m=2+\sqrt{15}\left(L\right)\\m=2-\sqrt{15}\left(TM\right)\end{matrix}\right.\)
Bài 8.
\(x^2-2x+m-3=0\)
\(\Delta=4-4\left(m-3\right)=-4m+16\)
a) Phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\Leftrightarrow-4m+16>0\Leftrightarrow m< 4\)
b) Áp dụng hệ thức Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Để \(x_1^2-2x_2+x_1x_2=16\Leftrightarrow x_1^2-\left(x_1+x_2\right)x_2+x_1x_2=16\)
\(\Leftrightarrow x_1^2-x_2^2=16\) \(\Leftrightarrow\left(x_1+x_2\right)\left(x_1-x_2\right)=16\Leftrightarrow x_1-x_2=8\)
Mà \(x_1+x_2=2\) \(\Rightarrow x_1=5;x_2=-3\Rightarrow x_1x_2=m-3=-15\Rightarrow m=-12\) (TM).