
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2A:
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
AH vuông góc BD
CK vuông góc BD
=>AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
=>AHCK là hình bình hành


1: Xét tứ giác BHCK có
CH//BK
BH//CK
Do đó: BHCK là hình bình hành
Suy ra: Hai đường chéo BC và HK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
2: Gọi giao điểm của IH và BC là O
Suy ra: IH\(\perp\)BC tại O và O là trung điểm của IH
Xét ΔHIK có
O là trung điểm của HI
M là trung điểm của HK
Do đó: OM là đường trung bình của ΔHIK
Suy ra: OM//IK
hay BC//IK
mà BC\(\perp\)IH
nên IH\(\perp\)IK
Xét ΔHOC vuông tại O và ΔIOC vuông tại O có
OC chung
HO=IO
Do đó: ΔHOC=ΔIOC
Suy ra: CH=CI
mà CH=BK
nên CI=BK
Xét tứ giác BCKI có IK//BC
nên BCKI là hình thang
mà CI=BK
nên BCKI là hình thang cân

\(a,\dfrac{x}{3x+6}=\dfrac{x}{3\left(x+2\right)}=\dfrac{x\left(x+2\right)}{3\left(x+2\right)^2}\\ \dfrac{5}{x^2+4x+4}=\dfrac{5}{\left(x+2\right)^2}=\dfrac{15}{3\left(x+2\right)^2}\\ b,\dfrac{5}{x^2-y^2+2x+1}=\dfrac{5}{\left(x-y+1\right)\left(x+y+1\right)}=\dfrac{5x}{x\left(x-y+1\right)\left(x+y+1\right)}\\ \dfrac{6}{x\left(x+y+1\right)}=\dfrac{6\left(x-y+1\right)}{x\left(x-y+1\right)\left(x+y+1\right)}\)
\(c,\dfrac{7x}{x^4-1}=\dfrac{7x}{\left(x^2+1\right)\left(x-1\right)\left(x+1\right)}=\dfrac{7x\left(x^2+1\right)}{\left(x^2+1\right)\left(x-1\right)\left(x+1\right)}\\ \dfrac{5x}{x^4+2x^2+1}=\dfrac{5x}{\left(x^2+1\right)^2}=\dfrac{5x\left(x-1\right)\left(x+1\right)}{\left(x^2+1\right)^2\left(x-1\right)\left(x+1\right)}\)

\(\left(x-3\right)\left(x^2+3x+9\right)+x\left(x+2\right)\left(2-x\right)=1\)
\(x^3-3^3+x\left(2^2-x^2\right)=1\)
\(x^3-27+4x-x^3=1\)
\(4x-27=1\)
\(4x=28\)
\(x=7\)
Vậy x = 7

c) Để A>-1 thì A+1>0
\(\Leftrightarrow\dfrac{1-x}{x+1}+1>0\)
\(\Leftrightarrow\dfrac{1-x+x+1}{x+1}>0\)
\(\Leftrightarrow\dfrac{2}{x+1}>0\)
mà 2>0
nên x+1>0
hay x>-1
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x>-1\\x\ne1\end{matrix}\right.\)
a) Ta có: \(A=\left(\dfrac{x+1}{x-1}-\dfrac{1-x}{x+1}+\dfrac{4x^2}{1-x^2}\right):\dfrac{2x^2-2}{x^2-2x+1}\)
\(=\left(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{\left(x-1\right)^2}{\left(x+1\right)\left(x-1\right)}-\dfrac{4x^2}{\left(x-1\right)\left(x+1\right)}\right):\dfrac{2\left(x^2-1\right)}{\left(x-1\right)^2}\)
\(=\dfrac{x^2+2x+1+x^2-2x+1-4x^2}{\left(x-1\right)\left(x+1\right)}:\dfrac{2\left(x-1\right)\left(x+1\right)}{\left(x-1\right)^2}\)
\(=\dfrac{-2x^2+2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{-2\left(x^2-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x-1}{2\left(x+1\right)}\)
\(=\dfrac{-2\cdot\left(x-1\right)}{2\left(x+1\right)}\)
\(=\dfrac{1-x}{x+1}\)

a: Xét ΔBAC có BI/BA=BE/BC
nên EI//AC và EI=1/2AC
=>EI vuông góc AB
DE vuông góc AB tại trung điểm của DE
=>D đối xứng E qua AB
b: Xét tứ giác DECA co
DE//CA
DE=CA(=2EI)
Do đó: DECA là hình bình hành
c: Xét tứ giác ADBE có
I là trung điểm chung của AB và DE
EA=EB
=>ADBE là hình thoi
e: Để ADBE là hình vuông thì góc AEB=90 độ
=>góc ABC=45 độ
Bạn tự vẽ hình nhé.
a) Do \(E\) đối xứng với \(D\) qua \(I\), do đó \(I\) là trung điểm của \(DE\) hay \(ID=IE\).
Ta cũng có : \(E\) là trung điểm của \(BC\), \(I\) là trung điểm của \(AB\) ⇒ \(IE\) là đường trung bình của \(\Delta ABC\) ⇒ \(IE // AC\). Lại có : \(AB\perp AC\) (giả thiết), vì vậy, \(IE\perp AB\).
Từ đó, suy ra \(AB\) là đường trung trực của \(DE\) hay \(D\) đối xứng với \(E\) qua \(AB\) (điều phải chứng minh).
b) Do \(IE\) là đường trung bình của \(\Delta ABC\) (chứng minh trên) nên \(IE=\dfrac{1}{2}AC\) và \(IE//AC\). Mặt khác, \(IE=\dfrac{1}{2}DE\). Suy ra được \(\dfrac{1}{2}AC=\dfrac{1}{2}DE\) hay \(AC=DE\). Suy ra, \(ADEC\) là hình bình hành (điều phải chứng minh).
c) Do \(I\) là trung điểm của \(DE\) (chứng minh trên) và của \(AB\) (giả thiết), suy ra \(ADBE\) là hình bình hành. Lại có \(AB\perp DE\) (do \(AB\) là đường trung trực của \(DE\) (chứng minh trên)). Suy ra, \(ADBE\) là hình thoi.
Do \(ADBE\) là hình thoi nên \(AE=EB=BD=DA=10(cm)\). Do đó, chu vi của hình thoi \(ADBE\) là \(C=AE+EB+BD+DA=4AE=4.10=40\left(cm\right)\).
d) Để hình thoi \(ADBE\) là hình vuông thì \(\hat{E}=90^o\) hay \(AE\) là đường cao của \(\Delta ABC\). Mà \(AE\) lại là đường trung tuyến của \(\Delta ABC\) (do \(E\) là trung điểm của \(BC\)). Để điều đó xảy ra thì \(\Delta ABC\) phải thêm điều kiện cân tại \(A\).

Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=$1-\sqrt{2};\sqrt{2}+1$1−√2;√2+1
Vậy A ko xảy ra GTLN
Để A đạt GTLN
=>x2 -2x đạt giá trị dương nhỏ nhất
=>x2-2x=1
=>x2-2x-1=0
=>x=\(1-\sqrt{2};\sqrt{2}+1\)
Vậy A ko xảy ra GTLN

Bài 1:
\(x^2-y^2-2y-1=x^2-\left(y^2+2y+1\right)=x^2-\left(y+1\right)^2=\left(x-y-1\right)\left(x+y+1\right)\)
Bài 2:
\(2\left(x+3\right)-x^2-3x=0\)
\(\Rightarrow2\left(x+3\right)-x\left(x+3\right)=0\Rightarrow\left(x+3\right)\left(2-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
Bài 3:
\(A=4x-x^2=-\left(x^2-4x+4\right)+4=-\left(x-2\right)^2+4\le4\)
\(maxA=4\Leftrightarrow x=2\)
Bài 4:
\(A\left(x\right)=2x^3-7x^2+5x+m=x^2\left(2x-3\right)-2x\left(2x-3\right)-x+m\)
\(=\left(2x-3\right)\left(x^2-2x\right)-x+m⋮B\left(x\right)=2x-3\)
\(\Rightarrow-x+m=0\Rightarrow m=x\)
Bài 5:
\(x+y=3\Rightarrow\left(x+y\right)^2=9\Rightarrow x^2+y^2=9-2xy=9-2.2=5\)
\(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=3\left(5-2\right)=9\)


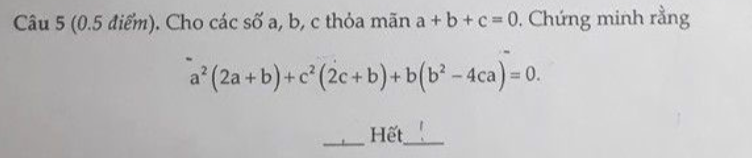

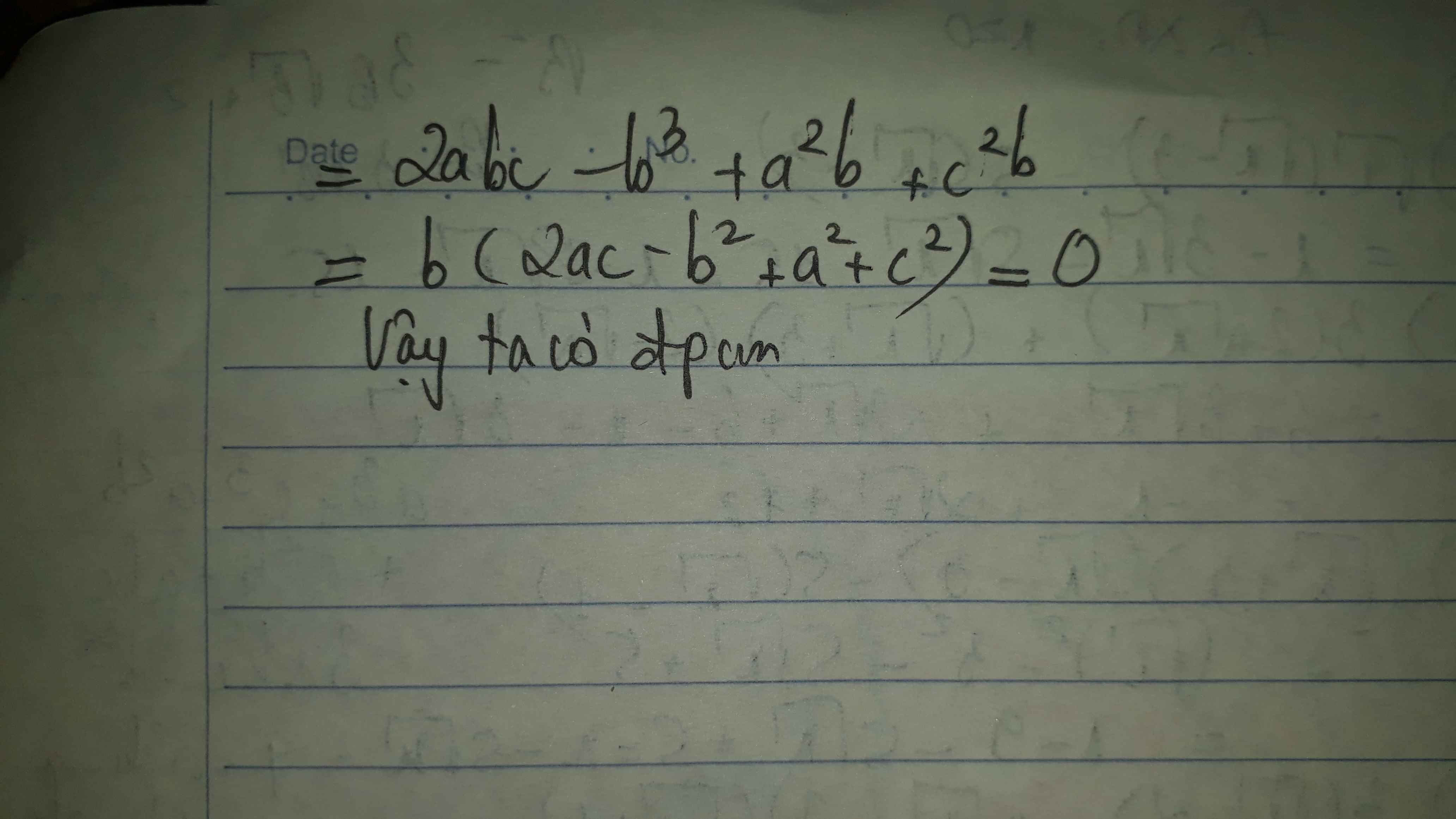

 iúp mình vs càng nhanh càng tốt ạ
iúp mình vs càng nhanh càng tốt ạ


a) Xét tam giác \(AEF\)và tam giác \(MEC\):
\(\widehat{AEF}=\widehat{MEC}\)(đối đỉnh)
\(\widehat{EAF}=\widehat{EMC}\left(=90^o\right)\)
suy ra \(\Delta AEF~\Delta MEC\left(g.g\right)\).
b) Xét tam giác \(BAC\)và tam giác \(BMF\):
\(\widehat{B}\)chung
\(\widehat{BAC}=\widehat{BMF}\left(=90^o\right)\)
suy ra \(\Delta BAC~\Delta BMF\left(g.g\right)\).
suy ra \(\frac{BA}{BM}=\frac{BC}{BF}\)
\(\Rightarrow BA.BF=BM.BC\)
c) \(BA.BF=BM.BC\Rightarrow\frac{BA}{BC}=\frac{BM}{BF}\)
Xét tam giác \(BAM\)và tam giác \(BCF\):
\(\frac{BA}{BC}=\frac{BM}{BF}\)
\(\widehat{B}\)chung
suy ra \(\Delta BAM~\Delta BFC\left(c.g.c\right)\)
\(\Rightarrow\widehat{BMA}=\widehat{BFC}\).
d) Đặt \(\frac{BF}{BM}=\frac{BC}{BA}=k\)
suy ra \(\frac{S_{BAC}}{S_{ABM}}=k^2\)
mà \(S_{AMCF}=3S_{ABM}\Rightarrow S_{ABC}=4S_{ABM}\Rightarrow k=2\).
\(\frac{BC}{BA}=2\Rightarrow tanB=2\Rightarrow\widehat{B}=arctan\left(2\right).\)