K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
10 tháng 10 2019
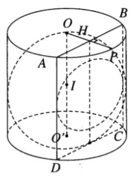
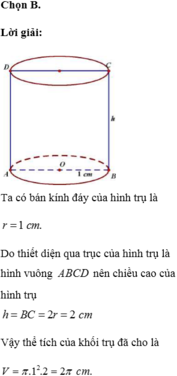
Trên mặt đáy tâm O ta gọi H là trung điểm của bán kính OP. Qua H kẻ dây cung AB ⊥ OP và nằm trong đáy (O; r). Các đường sinh AD và BC cùng với các dây cung AB và DC (thuộc đáy (O’, r)) xác định cho ta thiết diện cần tìm là một hình chữ nhật. Gọi S là diện tích hình chữ nhật này, ta có: SABCD= AB.AD trong đó AD = 2r còn AB = 2AH. Vì H là trung điểm của OP nên ta tính được AB = r 3 . Vậy S ABCD = 2 r 2 3



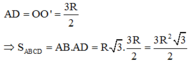
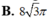



Bài 1:
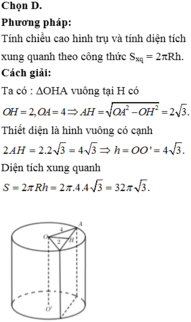
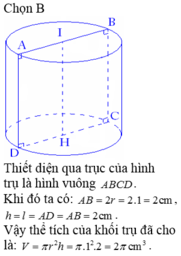
Vì mặt phẳng đi qua trục, cắt hình trụ theo thiết diện là hình vuông cạnh $a$ nên đây là hình trụ có chiều cao \(h=a\) và đường kính đáy \(2r=a\Rightarrow r=\frac{a}{2}\)
\(\Rightarrow \left\{\begin{matrix} S_{xq}=2\pi rh=2\pi. \frac{a}{2}.a=\pi a^2\\ S_{\text{đáy}}=\pi r^2=\pi.(\frac{a}{2})^2=\frac{1}{4}\pi a^2\end{matrix}\right.\)
\(S_{tp}=S_{xq}+2S_{\text{đáy}}=\pi a^2+\frac{1}{2}\pi a^2=\frac{3}{2}\pi a^2\) (đvdt)
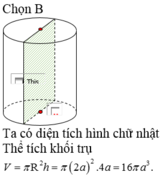
Bài 2:
\(S_{xq}=2\pi Rh=2\pi R.R\sqrt{3}=2\sqrt{3}\pi R^2\)
\(S_{\text{đáy}}=\pi R^2\)
\(\Rightarrow S_{tp}=S_{xq}+2S_{\text{đáy}}=2\sqrt{3}\pi R^2+2\pi R^2=2R^2\pi (\sqrt{3}+1)\)