
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: \(=14x^3-7x^2+28x-14x^3=-7x^2+28x\)
b: \(=\dfrac{3x^3-6x^2+2x^2-4x-x+2}{x-2}=3x^2+2x-1\)
c: \(\Leftrightarrow\left(2x-3-5x\right)\left(2x-3+5x\right)=0\)
=>(-3x-3)(7x-3)=0
=>x=-1 hoặc x=3/7

a: Ta có: \(\left(x+3\right)\left(x+4\right)\left(x+5\right)\left(x+6\right)+1\)
\(=\left(x^2+9x+18\right)\left(x^2+9x+20\right)+1\)
\(=\left(x^2+9x\right)^2+38\left(x^2+9x\right)+360+1\)
\(=\left(x^2+9x\right)^2+2\cdot\left(x^2+9x\right)\cdot19+19^2\)
\(=\left(x^2+9x+19\right)^2\)
b. \(x^2+y^2+2x+2y+2\left(x+1\right)\left(y+1\right)+2\)
\(=\left(x^2+2x+1\right)+2\left(x+1\right)\left(y+1\right)+\left(y^2+2y+1\right)\)
\(=\left(x+1\right)^2+2\left(x+1\right)\left(y+1\right)+\left(y+1\right)^2\)
\(=\left(x+1+y+1\right)^2=\left(x+y+2\right)^2\)
c. \(x^2-2x\left(y+2\right)+y^2+4y+4\)
\(=x^2-2x\left(y+2\right)+\left(y+2\right)^2\)
\(=\left(x-y-2\right)^2\)
d. \(x^2+2x\left(y+1\right)+y^2+2y+1\)
\(=x^2+2x\left(y+1\right)+\left(y+1\right)^2\)
\(=\left(x+y+1\right)^2\)

a: Ta có: \(\left(x^2+x-1\right)^2-\left(x^2+2x+3\right)^2\)
\(=\left(x^2+x-1-x^2-2x-3\right)\left(x^2+x-1+x^2+2x+3\right)\)
\(=\left(-x-4\right)\left(2x^2+3x+2\right)\)
b: Ta có: \(\left(x-3\right)^2-16\)
\(=\left(x-3-4\right)\left(x-3+4\right)\)
\(=\left(x+1\right)\left(x-7\right)\)
c: \(y^2+16y+64=\left(y+8\right)^2\)

\(\dfrac{x\left(x-8\right)+3\left(x+6\right)}{\left(x+6\right)\left(x-8\right)}=\dfrac{-12x+33}{\left(x+6\right)\left(x-8\right)}\left(đk:x\ne-6;8\right)\)
\(x^2-8x+3x+18=-12x+33\)
\(x^2-5x+18+12x-33=0\)
\(x^2+7x+15=0\)
\(\text{∆}=7^2-4.15=-11< 0\)
⇒ pt vô nghiệm
đk : x khác -6 ; 8
\(x^2-8x+3x+18=-12x+33\Leftrightarrow x^2+7x-25=0\)
\(\Leftrightarrow x=\dfrac{-7\pm\sqrt{149}}{2}\)

Số đo góc ngoài tại đỉnh D là:
\(180^0-360^0+70^0+90^0+120^0=100^0\)
CM:(n-1)^2(n+1)+(n-1)(n+1) chia hết cho 6 với 1 số nguyên n. Mng giúp mình vs ạ. Mình c.on nhiều ạaa

\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left[\left(n-1\right)+1\right]\)
\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)
\(=n\left(n-1\right)\left(n+1\right)\)
Xét:
\(n\left(n-1\right)\) là hai số tự nhiên liên tiếp nên sẽ có số chẵn nên sẽ chia hết cho 2
\(n\left(n-1\right)\left(n+1\right)\) là 3 số tự nhiên liên tiếp nên sẽ chia hết cho 3
Mà: (2;3)=1 nên
\(n\left(n-1\right)\left(n+1\right)\) sẽ chia hết cho 2 x 3 = 6 (đpcm)
\(\left(n-1\right)^2\left(n+1\right)+\left(n-1\right)\left(n+1\right)\)
\(=\left(n-1\right)\left(n+1\right)\left(n-1+1\right)\)
\(=\left(n-1\right)n\left(n+1\right)\) là 3 số tự nhiên liên tiếp
\(\Rightarrow\left\{{}\begin{matrix}\left(n-1\right)n\left(n+1\right)⋮2\\\left(n-1\right)n\left(n+1\right)⋮3\end{matrix}\right.\)
\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮\left(2.3\right)\)
mà \(UCLN\left(2;3\right)=1\)
\(\Rightarrow\left(n-1\right)n\left(n+1\right)⋮6\)
\(\Rightarrow dpcm\)

a) Ta có: \(2x+x^2=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
b) Ta có: \(\left(2x+1\right)^2-25=0\)
\(\Leftrightarrow\left(2x-4\right)\left(2x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)

a) \(5x+10y=5\left(x+2y\right)\)
b) \(3x^2y+9xy^2z=3xy\left(x+3yz\right)\)
g) \(x^2-x-6=\left(x-3\right)\left(x+2\right)\)
h) \(x^2+9x+8=\left(x+8\right)\left(x+1\right)\)
l) \(x^2-10x+9=\left(x-1\right)\left(x-9\right)\)
k) \(x^2+x-12=\left(x+4\right)\left(x-3\right)\)
l) \(3x^2+8x+4=\left(3x+2\right)\left(x+2\right)\)



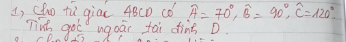 giúp, mình vs ạ, mình cảm tạ ạ
giúp, mình vs ạ, mình cảm tạ ạ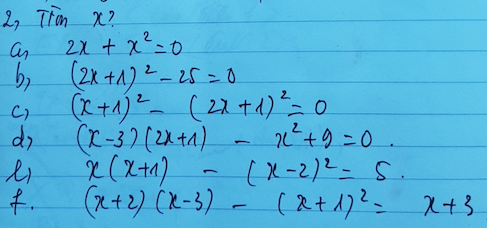
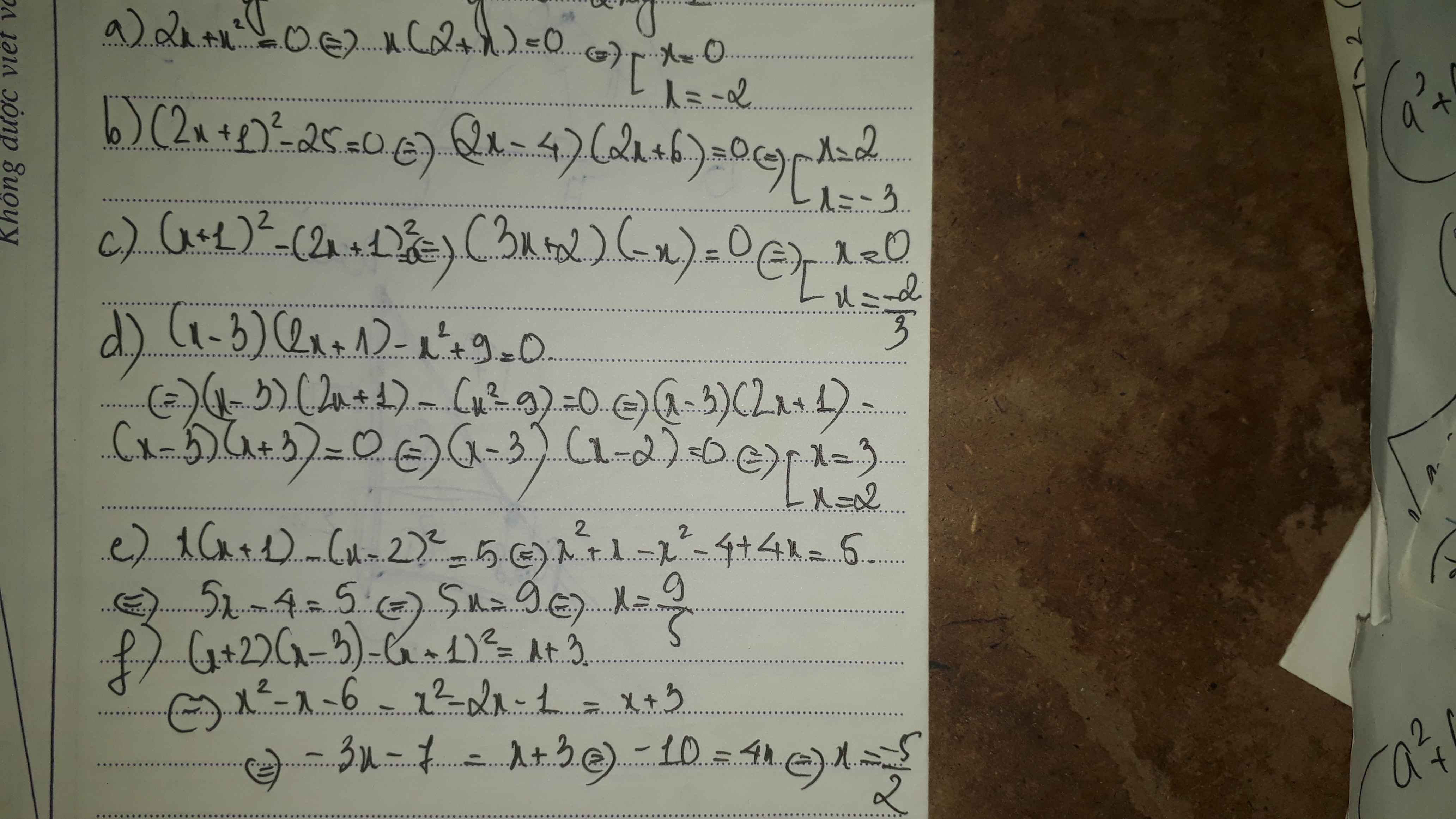
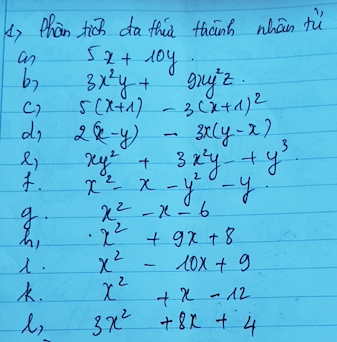
b: \(A=\dfrac{x^2+2+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x^2+x+1}\)
Có thể chỉ thêm cho em tại sao điều kiện xác định lại thế ko ạ?