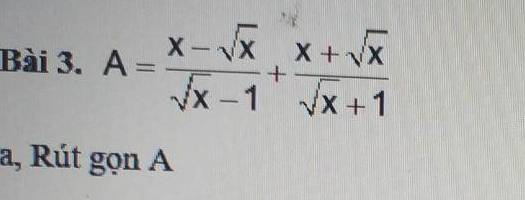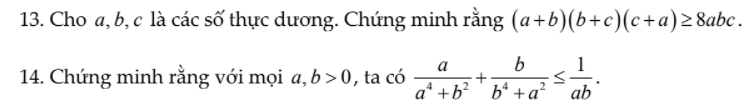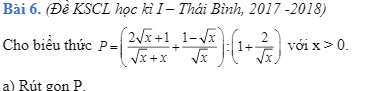Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)



7:
a: \(P=\left(1:\dfrac{x-x+1}{\sqrt{x}+\sqrt{x-1}}-\dfrac{x-1-2}{\sqrt{x-1}-\sqrt{2}}\right)\cdot\left(\dfrac{2\sqrt{x}-\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\right)\)\(=\left(\sqrt{x}+\sqrt{x-1}-\sqrt{x-1}-\sqrt{2}\right)\cdot\dfrac{\sqrt{x}-\sqrt{2}}{\sqrt{x}\left(\sqrt{2}-\sqrt{x}\right)}\)
\(=-\dfrac{\left(\sqrt{x}-\sqrt{2}\right)}{\sqrt{x}}\)
b: Khi x=3-2căn 2 thì \(P=-\dfrac{\sqrt{2}-1-\sqrt{2}}{\sqrt{2}-1}=\dfrac{1}{\sqrt{2}-1}=\sqrt{2}+1\)

\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)

1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)

\(P=\dfrac{2\sqrt{x}+1+\left(1-\sqrt{x}\right)\left(1+\sqrt{x}\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+1+1-x}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}}{\sqrt{x}+2}=\dfrac{-x+2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}=\dfrac{-x+2\sqrt{x}+2}{x+3\sqrt{x}+2}\)

Ta có 1ml = 1cm3
Vậy thể tích của lọ đựng dung dịch đó là 100 cm3
Diện tích trong của đáy lọ là:
Ta có: V = S đáy * h => S đáy = V : h = 100 : 12.5 = 8 (cm2)

 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn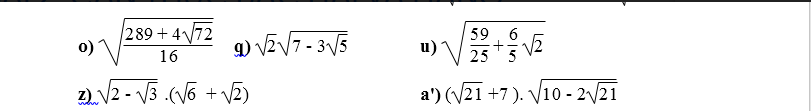


 Giúp mình giải 2 câu này với. Mình cảm ơn
Giúp mình giải 2 câu này với. Mình cảm ơn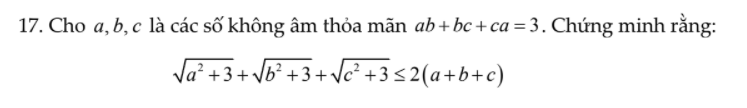 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.