K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DQ
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 8 2023
\(\dfrac{x}{9}\) < \(\dfrac{4}{7}\) < \(x\) + \(\dfrac{1}{9}\)
\(\dfrac{7x}{63}\) < \(\dfrac{36}{63}\) < \(\dfrac{63x}{63}\) + \(\dfrac{7}{63}\)
7\(x\) < 36 < 63\(x\) + 7
⇒\(\left\{{}\begin{matrix}7x< 36\\63x+7>36\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\63x>36-7\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\63x>29\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\x>\dfrac{29}{63}\end{matrix}\right.\)
\(\dfrac{29}{63}\)< \(x\) < \(\dfrac{36}{7}\) vì \(x\in\) Z nên \(x\in\) { 1; 2; 3; 4; 5}
⇒ \(\dfrac{x}{9}\) = \(\dfrac{1}{9}\); \(\dfrac{2}{9}\); \(\dfrac{3}{9}\); \(\dfrac{4}{9}\);\(\dfrac{5}{9}\)
NX
9 tháng 8 2023
\(\dfrac{x}{9}< \dfrac{4}{7}< \dfrac{x+1}{9}\)
=>\(\dfrac{7x}{63}< \dfrac{36}{63}< \dfrac{7x+7}{63}\)
\(\Rightarrow7x< 36< 7x+7\)
\(\Rightarrow x< \dfrac{36}{7}< x+1\)
\(\Rightarrow x< 5\dfrac{1}{7}< x+1\)
\(\Rightarrow x=5\)
DN
1
ND
Nguyễn Đức Trí
VIP
7 tháng 8 2023
\(P=\left(x+5\right)\left(ax^2+bx+25\right)\) (Sửa =25 thành +25)
\(Q=x^3+125=x^3+5^3=\left(x+5\right)\left(x^2-5x+25\right)\) (Sửa =25 thành +25)
Để \(P=Q\Rightarrow\left(ax^2+bx+25\right)=\left(x^2-5x+25\right)\)
\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-5\end{matrix}\right.\)
21 tháng 9 2020
\(A=\frac{3x-1}{x-1}=\frac{3\left(x-1\right)+2}{x-1}=3+\frac{2}{x-1}\)
\(B=\frac{2x^2+x-1}{x+2}=\frac{\left(x+2\right)\left(2x-3\right)+5}{x+2}=2x-3+\frac{5}{x+2}\)
Để A,B đều là số nguyên thì \(x-1\in\left\{1;2;-1;-2\right\}\) và \(x+2\in\left\{1;5;-1;-5\right\}\)
Bạn tự làm nốt
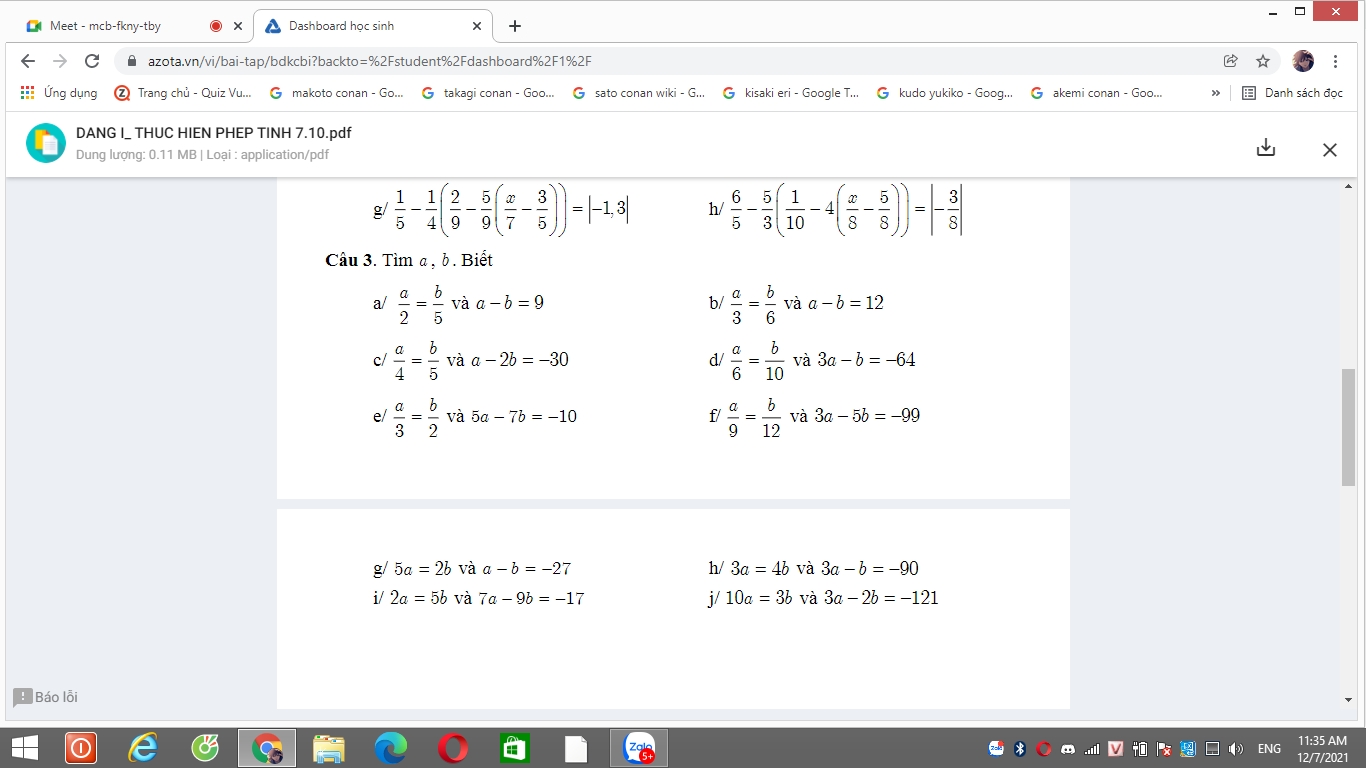
Câu 3:
\(a,\dfrac{a}{2}=\dfrac{b}{5}=\dfrac{a-b}{2-5}=\dfrac{9}{-3}=-3\\ \Rightarrow\left\{{}\begin{matrix}a=-6\\b=-15\end{matrix}\right.\\ b,\dfrac{a}{3}=\dfrac{b}{6}=\dfrac{a-b}{3-6}=\dfrac{12}{-3}=-4\\ \Rightarrow\left\{{}\begin{matrix}a=-12\\b=-24\end{matrix}\right.\\ c,\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{a-2b}{4-10}=\dfrac{-30}{-6}=5\\ \Rightarrow\left\{{}\begin{matrix}a=20\\b=25\end{matrix}\right.\)