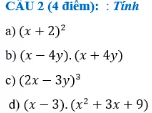Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho tam giác ABC cân tại A.Hai đường trung tuyến BD,CE cắt nhau tại G.Trên tia đối của tia DB lấy điểm F sao cho DF=1/3BD.Trên tia đối của tia EC lấy điểm H sao cho EH=1/3EC.Chứng minh tứ giác BCFH là hình chữ nhật.

Gọi tứ giác là ABCD,O là giao điểm của 2 đường chéo
Xét t/g AOB có: OA+OB>AB
Xét t/g BOC có: OB+OC>BC
Xét t/g COD có: OC+OD>CD
Xét t/g AOD có: OA+OD>DA
Do đó: OA+OB+OB+OC+OC+OD+OD+OA>AB+BC+CD+DA
=>2(OA+OB+OC+OD)>AB+BC+CD+DA
=>AC+BD > \(\frac{AB+BC+CD+DA}{2}\) (1)
Xét t/g ABC có: AB+BC > AC
Xét t/g BDC có: BC+DC > BD
Xét t/g CDA có: CD+AD > AC
Xét t/g DAB có: DA+AB > BD
Do đó AB+BC+BC+CD+CD+AD+DA+AB > AC+BD+AC+BD
=>2(AB+BC+CD+DA) > 2(AC+BD)
=>AB+BC+CD+DA > AC+BD (2)
Từ (1) và (2) => đpcm

Gọi 3 số tự nhiên liên tiếp là : \(x;x+1;x+2\left(x\in N\right)\)
Theo bài ra ta có :
\(\left(x+1\right)\left(x+2\right)-x\left(x+1\right)=140\)
\(\Rightarrow x^2+x+2x+2-x^2-x=140\)
\(\Rightarrow2x+2=140\)
\(\Rightarrow2\left(x+1\right)=140\)
\(\Rightarrow x+1=70\)
\(\Rightarrow x=69\)
\(\Rightarrow\hept{\begin{cases}x+1=70\\x+2=71\end{cases}}\)
Vậy 3 số cần tìm là : 69 ; 70 ; 71

\(19+x\left(x-2\right)^2=\left(x+3\right)\left(x^2-3x+9\right)\)
\(\Leftrightarrow\left(x-\frac{3}{2}\right)^2+\frac{27}{4}=0\)
Vậy phương trình vô nghiệm
=> 19+x(x-2)^2 = x^3+3^3 ( theo hằng đẳng thức thứ 6 )
=> 19 + x(x^2-4x+4) = x^3 +3^3
=> 19 + x^3 - 4x^2 + 4x = x^3 + 3^3
=> x^3 - 4x^2 + 4x + 19 = x^3 + 3^3(vô lí )
Vậy đa thức 0 có x thỏa mãn

a) \(\left(x+2\right)^2=x^2+4x+4\)
b) \(\left(x-4y\right)\left(x+4y\right)=x^2-\left(4y\right)^2=x^2-16y^2\)
c) \(\left(2x-3y\right)^3=\left(2x\right)^3-3\cdot\left(2x\right)^2\cdot\left(3y\right)+3\cdot\left(2x\right)\cdot\left(3y\right)^2-\left(3y\right)^3\)
\(=8x^3-36x^2y+1587xy^2-27y^3\)
d) \(\left(x-3\right)\left(x^2+3x+9\right)=x^3-3^3=x^3-27\)