
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, M(x)= 3x^3 - 2x^2 + 1 (đã rút gọn ) , ý b bạn chỉ cần thay M(-1) và M(2) vào x lần lượt từng con là đc vd : M(-1)= 3* (-1^3) - 2* (- 1)^2 + 1 rồi tính ra kết quả là được

`@` `\text {Ans}`
`\downarrow`
`c)`
\(2-3^{x-1}-7=11\)
`\Rightarrow`\(3^{x-1}-5=11\)
`\Rightarrow`\(3^{x-1}=11+5\)
`\Rightarrow`\(3^{x-1}=16\)
Bạn xem lại đề
`d)`
\(\left(x-\dfrac{3}{5}\right)\div\dfrac{-1}{3}=-0,4\)
`\Rightarrow`\(x-\dfrac{3}{5}=-0,4\cdot\left(-\dfrac{1}{3}\right)\)
`\Rightarrow`\(x-\dfrac{3}{5}=\dfrac{2}{15}\)
`\Rightarrow`\(x=\dfrac{2}{15}+\dfrac{3}{5}\)
`\Rightarrow`\(x=\dfrac{11}{15}\)
Vậy, \(x=\dfrac{11}{15}\)

Áp dụng t/c dtsbn:
\(\dfrac{a+b-c}{c}=\dfrac{a-b+c}{b}=\dfrac{-a+b+c}{a}=\dfrac{a+b-c+a-b+c-a+b+c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-c=c\\a-b+c=b\\-a+b+c=a\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\)
\(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2a.2b.2c}{abc}=8\)


\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left\{\dfrac{7}{12}-\left[\dfrac{15}{21}-\left(\dfrac{1}{3}-\dfrac{5}{4}\right)-\left(\dfrac{2}{7}+\dfrac{1}{3}\right)\right]\right\}\)
 \(B=\dfrac{3}{2}-\dfrac{2}{21}-\left\{\dfrac{7}{12}-\left[\dfrac{15}{21}-\left(-\dfrac{11}{12}\right)-\dfrac{13}{21}\right]\right\}\)
\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left\{\dfrac{7}{12}-\left[\dfrac{15}{21}-\left(-\dfrac{11}{12}\right)-\dfrac{13}{21}\right]\right\}\)
\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left\{\dfrac{7}{12}-\dfrac{85}{84}\right\}\)
\(B=\dfrac{3}{2}-\dfrac{2}{21}-\left(-\dfrac{3}{7}\right)\)
\(B=\dfrac{11}{6}\)

\(=\dfrac{3}{2}-\dfrac{2}{21}-\dfrac{7}{12}+\left[\dfrac{15}{21}-\dfrac{1}{3}+\dfrac{5}{4}-\dfrac{2}{7}-\dfrac{1}{3}\right]\)
=11/12-2/21+5/7-2/3+5/4-2/7
=11/12-2/3+5/4-2/21+3/7
=11/12-8/12+15/12-2/21+9/21
=18/12+7/21
=3/2+1/3
=9/6+2/6=11/6

Cái này bạn lên mạng search có nhiều mà. Nguyên cái video hướng dẫn đó.

Đề:........
<=> (24)x < (27)4
<=> 24x < 228
<=> 4x < 28
<=> x < 7
Vậy x = {0; 1; 2; 3; 4; 5; 6}

a) Do \(\left(3x-\dfrac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\)
\(minA=-4\Leftrightarrow x=\dfrac{1}{6}\)
b) Do \(\left(2x+1\right)^4\ge0\forall x,\left(y-\dfrac{1}{2}\right)^6\ge0\forall y\)
\(\Rightarrow B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\)
\(minB=0\Leftrightarrow\)\(\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
a: \(A=\left(3x-\dfrac{1}{2}\right)^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{6}\)
b: \(B=\left(2x+1\right)^4+3\left(y-\dfrac{1}{2}\right)^6\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\)

x/2 = y/3 = k => x = 2k; y = 3k
xy = 54
2k . 3k = 54
6k^2 = 54 => k^2 = 9 => k = 3 hoặc -3
*k = 3 => x = 2.3=6; y = 3.3=9
*k = -3 => x=2.(-3)=-6; y=3.(-3)=-9
Vậy x=6; y=9
x=-6; y=-9
Bạn k cho mình nha, mình mới tham gia Online math nên ít điểm lắm.
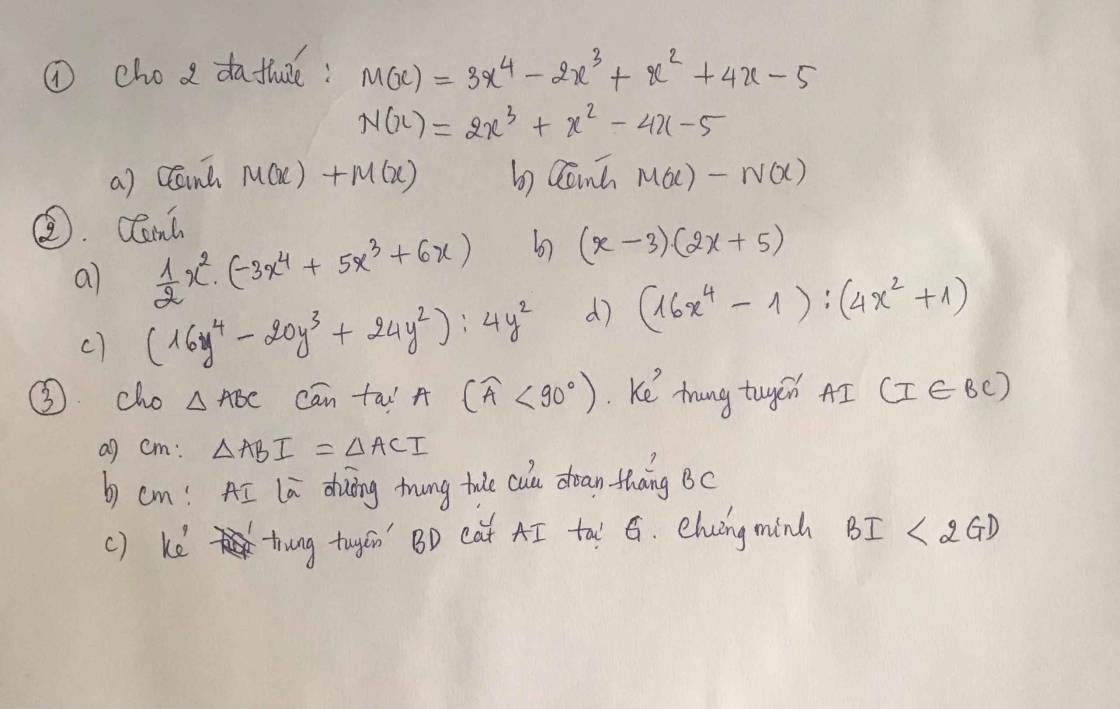


 giúp mình 2 câu này với ạ mình đang cần gấp
giúp mình 2 câu này với ạ mình đang cần gấp
Câu 3:
a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
b: ΔAIB=ΔAIC
=>\(\widehat{AIB}=\widehat{AIC}\)
mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)
nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)
=>AI\(\perp\)BC
mà I là trung điểm của BC
nên AI là đường trung trực của BC
c: Xét ΔABC có
AI,BD là các đường trung tuyến
AI cắt BD tại G
Do đó: G là trọng tâm của ΔABC
=>BG=2GD
mà BG>BI(ΔGIB vuông tại I)
nên BI<2GD
Bài 2:
a: \(\dfrac{1}{2}x^2\left(-3x^4+5x^3+6x\right)\)
\(=-\dfrac{1}{2}x^2\cdot3x^4+\dfrac{1}{2}x^2\cdot5x^3+\dfrac{1}{2}x^2\cdot6x\)
\(=-\dfrac{3}{2}x^6+\dfrac{5}{2}x^5+3x^3\)
b: \(\left(x-3\right)\left(2x+5\right)\)
\(=2x^2+5x-6x-15\)
\(=2x^2-x-15\)
c: \(\dfrac{\left(16y^4-20y^3+24y^2\right)}{4y^2}\)
\(=\dfrac{16y^4}{4y^2}-\dfrac{20y^3}{4y^2}+\dfrac{24y^2}{4y^2}\)
\(=4y^2-5y+6\)
d: \(\dfrac{16x^4-1}{4x^2+1}=\dfrac{\left(4x^2-1\right)\left(4x^2+1\right)}{4x^2+1}=4x^2-1\)