
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: XétΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔAMI vuông tại I và ΔADI vuông tại I có
AI chung
MI=DI
Do đó: ΔAMI=ΔADI
Suy ra: AM=AD
vì AM⊥BC tại M
=>ΔABM vuông tại M và ΔACM vuông tại M
XétΔABM vuông tại M và ΔACM vuông tại M ta có
AB=AC
\(\widehat{AMB}=\widehat{AMC=90^o}\)
cạnh AM chung
=> ΔABM=ΔACM(c.h-c.g.v)
ta có MI⊥AC
==>t ΔAMI vuông tại I và ΔADI vuông tại I
Xét ΔAMI vuông tại I và ΔADI vuông tại I ta có
AI chung
\(\widehat{AIM}=\widehat{AID}=90^o\)
MI=DI
==>ΔAMI=ΔADI
==> AM=AD(2 cạnh tg ứng)

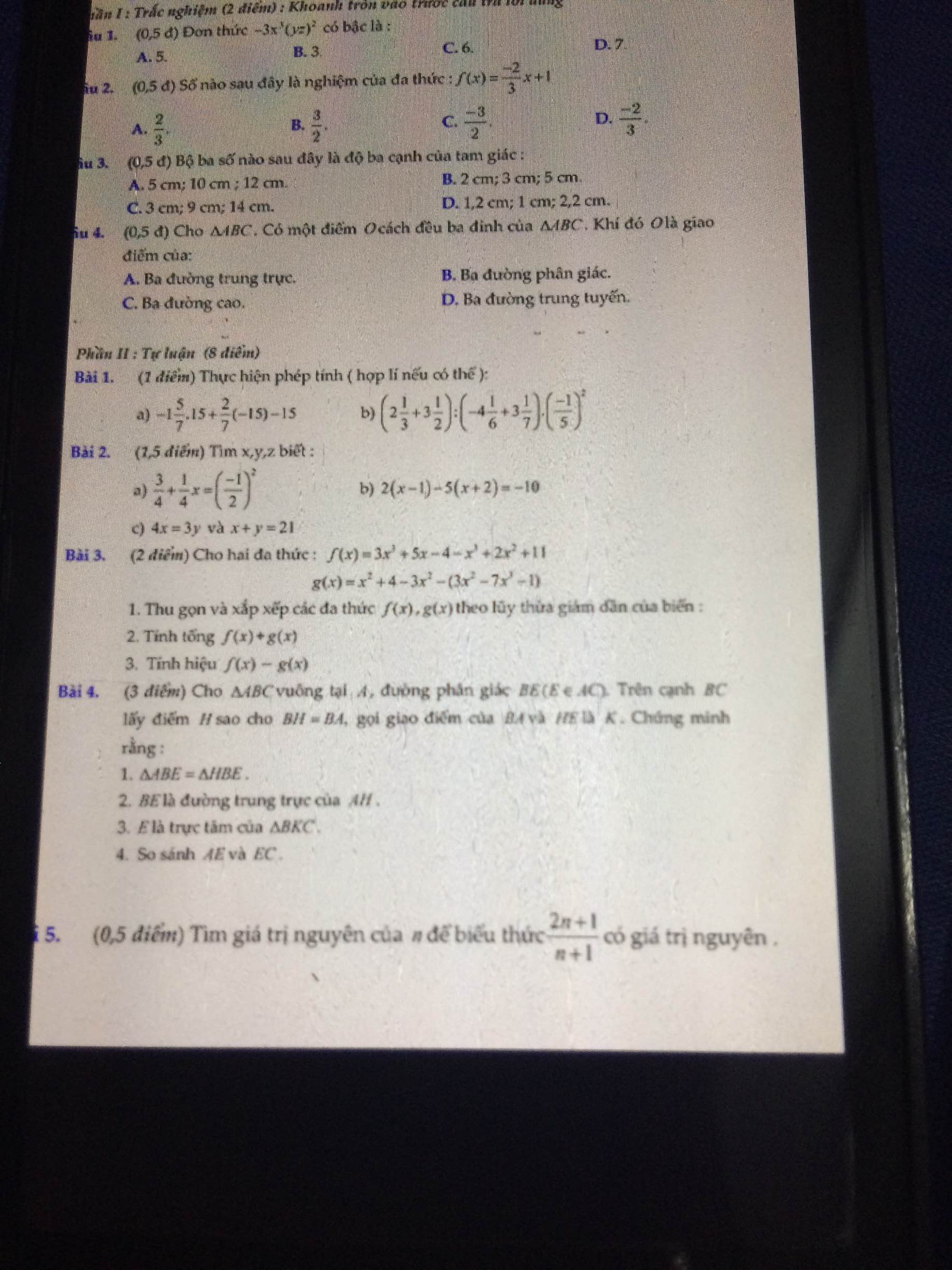
Bài 4:
a) Xét ΔABE và ΔHBE có
BA=BH(gt)
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
BE chung
Do đó: ΔABE=ΔHBE(c-g-c)
b) Ta có: ΔABE=ΔHBE(cmt)
nên EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(gt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c) Ta có: ΔABE=ΔHBE(cmt)
nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(gt)
nên \(\widehat{BHE}=90^0\)
Xét ΔBKC có
KH là đường cao ứng với cạnh BC
CA là đường cao ứng với cạnh BK
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)
d) Ta có: EA=EH(cmt)
mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)
nên EA<EC

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a-3b}{2\cdot5-3\cdot2}=\dfrac{12}{4}=3\)
Do đó: a=15; b=6
d) Áp dụng t/c dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a}{10}=\dfrac{3b}{6}=\dfrac{2a-3b}{10-6}=\dfrac{12}{4}=3\)
\(\Rightarrow\left\{{}\begin{matrix}a=3.5=15\\b=3.2=6\end{matrix}\right.\)
f) \(\Rightarrow\dfrac{x}{5}=\dfrac{y}{3}=-\dfrac{z}{2}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{-z}{2}=\dfrac{x+y-z}{5+3+2}=\dfrac{2}{10}=\dfrac{1}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}.5=1\\y=\dfrac{1}{5}.3=\dfrac{3}{5}\\z=\dfrac{1}{5}.\left(-2\right)=-\dfrac{2}{5}\end{matrix}\right.\)
g) \(\dfrac{x}{4}=\dfrac{y}{5}=k\)\(\Rightarrow\left\{{}\begin{matrix}x=4k\\y=5k\end{matrix}\right.\)
\(\Rightarrow xy=20k^2=500\Rightarrow k=\pm5\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=20\\y=25\end{matrix}\right.\\\left\{{}\begin{matrix}x=-20\\y=-25\end{matrix}\right.\end{matrix}\right.\)

Bài 5:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{120}{12}=10\)
Do đó: a=30; b=40; c=50

6:
a: \(\Leftrightarrow\dfrac{\sqrt{4}-\sqrt{1}}{4-1}+\dfrac{\sqrt{7}-\sqrt{4}}{7-4}+...+\dfrac{\sqrt{3n+4}-\sqrt{3n+1}}{3}=8\)
=>\(-\sqrt{1}+\sqrt{4}-\sqrt{4}+\sqrt{7}-...-\sqrt{3n+1}+\sqrt{3n+4}=24\)
=>\(\sqrt{3n+4}=24+1=25\)
=>3n+4=625
=>3n=621
=>n=207
b: \(\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+...+\dfrac{1}{\left(n+1\right)\sqrt{n}+n\cdot\sqrt{n+1}}=\dfrac{4}{5}\)
=>\(\dfrac{1}{\sqrt{1}}-\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{n}}-\dfrac{1}{\sqrt{n+1}}=\dfrac{4}{5}\)
=>\(1-\dfrac{1}{\sqrt{n+1}}=\dfrac{4}{5}\)
=>n+1=25
=>n=24

d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC





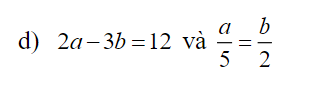

 giúp mình với ạ câu nào cũng được ạ
giúp mình với ạ câu nào cũng được ạ
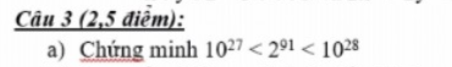

a: XétΔABM vuông tại M và ΔACM vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔAMI vuông tại I và ΔADI vuông tại I có
AI chung
MI=DI
Do đó: ΔAMI=ΔADI
Suy ra: AM=AD