K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 12 2021
a: Xét (O) có
ΔBFC nội tiếp
BC là đường kính
Do đó: ΔBFC vuông tại F
30 tháng 5 2021
Mọi người giúp mình với mình đang cần gấp mình cảm ơn nhiều ạ
7 tháng 7 2021
a)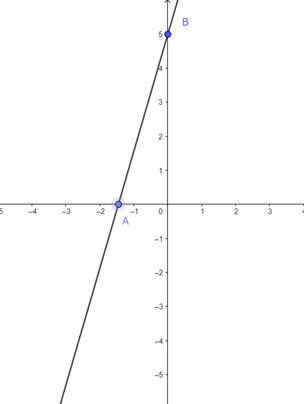 
b) \(tanOAB=\dfrac{OB}{OA}=\dfrac{5}{\dfrac{5}{3}}=3\Rightarrow\widehat{OAB}=71^o34'\)
21 tháng 7 2021
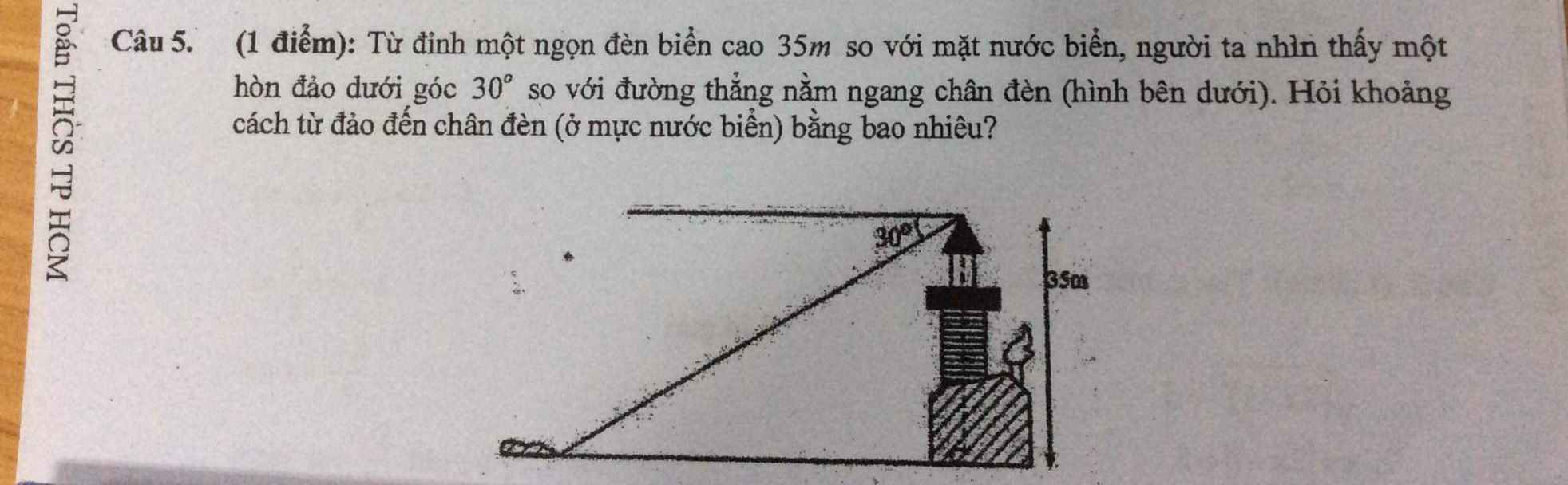
Ta coi hình vẽ là tam giác ABC vuông tại A với B là đỉnh ngọn đèn
góc BCA=30o(2 góc so le trong)
Theo tỉ số lượng giác trong tam giác vuông ta có:
CA=AB : tanC30
CA=35:tan30=60,6(m)
Vậy khoảng cách từ chân đèn đến hòn đảo là 60,6m
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 7 2021
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=7\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
23 tháng 7 2021
Ta có: \(\sqrt{x^2-4x+4}-5=2\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
HN
1
22 tháng 9 2021
a: Ta có: \(A=\sqrt{4-\sqrt{15}}\cdot\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\)
\(=\sqrt{8-2\sqrt{15}}\cdot\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=\left(8-2\sqrt{15}\right)\left(4+\sqrt{15}\right)\)
\(=32+8\sqrt{15}-8\sqrt{15}-30\)
\(=2>\sqrt{3}\)
23 tháng 7 2021
b) Đặt (d3): y=ax+b
Vì (d3)//(d1) nên \(a=-\dfrac{2}{3}\)
Vậy: (d3): \(y=\dfrac{-2}{3}x+b\)
Thay x=6 vào (d2), ta được:
\(y=-2\cdot6+4=-12+4=-8\)
Thay x=6 và y=-8 vào (d3), ta được:
\(\dfrac{-2}{3}\cdot6+b=-8\)
\(\Leftrightarrow b=-4\)
Vậy: (d3): \(y=\dfrac{-2}{3}x-4\)
23 tháng 7 2021
a) Ta có: \(\sqrt{12+2\sqrt{35}}-\sqrt{12-2\sqrt{35}}\)
\(=\sqrt{7}+\sqrt{5}-\sqrt{7}+\sqrt{5}\)
\(=2\sqrt{5}\)
b) Ta có: \(\left(\dfrac{5+\sqrt{5}}{\sqrt{5}+1}+2\right)\left(\dfrac{5-\sqrt{5}}{\sqrt{5}-1}-2\right)\)
\(=\left(\sqrt{5}+2\right)\left(\sqrt{5}-2\right)\)
=1
c) Ta có: \(\dfrac{7\sqrt{2}+2\sqrt{7}}{\sqrt{14}}-\dfrac{5}{\sqrt{7}+\sqrt{2}}\)
\(=\sqrt{7}+\sqrt{2}-\sqrt{7}+\sqrt{2}\)
\(=2\sqrt{2}\)
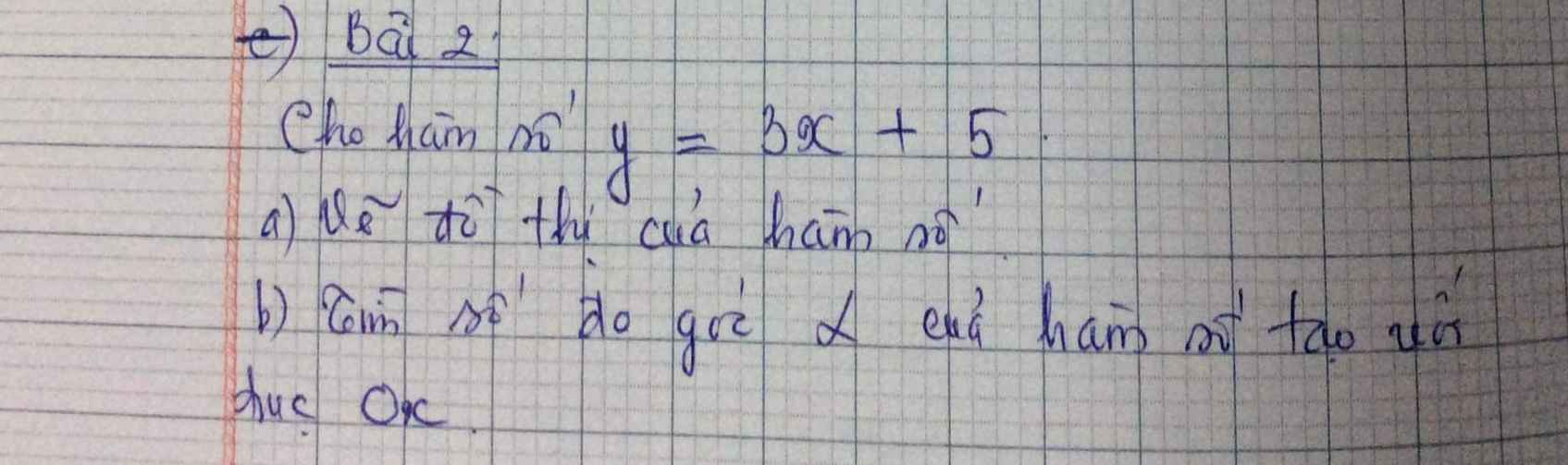
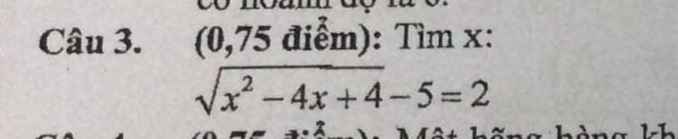
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của BA(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra MO⊥AB
đã ghi rõ là giúp mình câu b mà sao tự nhiên.....