
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



2.1
\(\Leftrightarrow x^3+3x^2+2x-3x^2-9x-6=0\)
\(=x\left(x^2+3x+2\right)-3\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)
2.2
\(\Leftrightarrow x^3-2x^2-2x-x^2+2x+2=0\)
\(\Leftrightarrow x\left(x^2-2x-2\right)-\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-2x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=1\pm\sqrt{3}\end{matrix}\right.\)
2.3
\(\Leftrightarrow3x^3-3x^2+2x+3x^2-3x+2=0\)
\(\Leftrightarrow x\left(3x^2-3x+2\right)+3x^2-3x+2=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2-3x+2\right)=0\)
\(\Leftrightarrow x=-1\)
2.5
\(\Leftrightarrow2x^3+x^2+3x-4x^2-2x-6=0\)
\(\Leftrightarrow x\left(2x^2+x+3\right)-2\left(2x^2+x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x^2+x+3\right)=0\)
\(\Leftrightarrow x=2\)

Câu 1:\(x^2.y+x.y^2-x-y=x.\left(x.y-1\right)+y.\left(x.y-1\right)=\left(x+y\right).\left(x.y-1\right)\)
Câu 3:\(a.x^2+a.y-b.x^2-b.y=x^2.\left(a-b\right)+y.\left(a-b\right)=\left(x^2+y\right).\left(a-b\right)\)

`a)2x^2+3(x-1)(x+1)=5x(x+1)`
`<=>2x^2+3x^2-3=5x^2+5x`
`<=>5x=-3`
`<=>x=-3/5`
__________________________________________
`b)(x-3)^3+3-x=0` nhỉ?
`<=>(x-3)^3-(x-3)=0`
`<=>(x-3)(x^2-1)=0`
`<=>[(x=3),(x^2=1<=>x=+-1):}`
__________________________________________
`c)5x(x-2000)-x+2000=0`
`<=>5x(x-2000)-(x-2000)=0`
`<=>(x-2000)(5x-1)=0`
`<=>[(x=2000),(x=1/5):}`
__________________________________________
`d)3(2x-3)+2(2-x)=-3`
`<=>6x-9+4-2x=-3`
`<=>4x=2`
`<=>x=1/2`
__________________________________________
`e)x+6x^2=0`
`<=>x(1+6x)=0`
`<=>[(x=0),(x=-1/6):}`

Bài 2:
3) ĐKXĐ: \(x\ge1\)Ta có: \(\sqrt{49x-49}-\sqrt{25x-25}=3\)
\(\Leftrightarrow7\sqrt{x-1}-5\sqrt{x-1}=3\)
\(\Leftrightarrow2\sqrt{x-1}=3\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{3}{2}\)
\(\Leftrightarrow x-1=\dfrac{9}{4}\)
hay \(x=\dfrac{13}{4}\)(thỏa ĐK)
Vậy: \(S=\left\{\dfrac{13}{4}\right\}\)
4) Ta có: \(1+\dfrac{3\left(x-5\right)}{4}>\dfrac{2x-1}{6}-2\)
\(\Leftrightarrow\dfrac{12}{12}+\dfrac{9\left(x-5\right)}{12}-\dfrac{2\left(2x-1\right)}{12}-\dfrac{24}{12}>0\)
\(\Leftrightarrow12+9x-45-4x+2-24>0\)
\(\Leftrightarrow5x-55>0\)
\(\Leftrightarrow5x>55\)
hay x>11
Vậy: S={x|x>11}
5) Ta có: \(\dfrac{2x+3}{x^2+1}< 0\)
mà \(x^2+1>0\forall x\)
nên 2x+3<0
\(\Leftrightarrow2x< -3\)
hay \(x< -\dfrac{3}{2}\)
Vậy: S={x|\(x< -\dfrac{3}{2}\)}


Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)


1:
a: Xét ΔABC vuông tại A và ΔKBA vuông tại K có
góc ABC chung
=>ΔABC đồng dạngvới ΔKBA
b: Xét ΔABC vuông tại A có AK là đường cao
nên CA^2=CK*CB
c: Xét ΔBAD vuôg tại A và ΔBKI vuông tại K có
góc ABD=góc KBI
=>ΔBAD đồng dạngvới ΔBKI
=>BA/BK=BD/BI
=>BA*BI=BK*BD
d: IK/BK=BK/BA=BA/BC=AD/DC=2/3
=>2,5/DC=2/3
=>DC=3,75cm
=>AC=6,25cm
Đặt BA/2=BC/3=k
=>BA=2k; BC=3k
BC^2-AB^2=AC^2
=>5k^2=6,25^2
=>\(k=\dfrac{5\sqrt{5}}{4}\)
=>\(BA=\dfrac{5\sqrt{5}}{2}\left(cm\right)\)
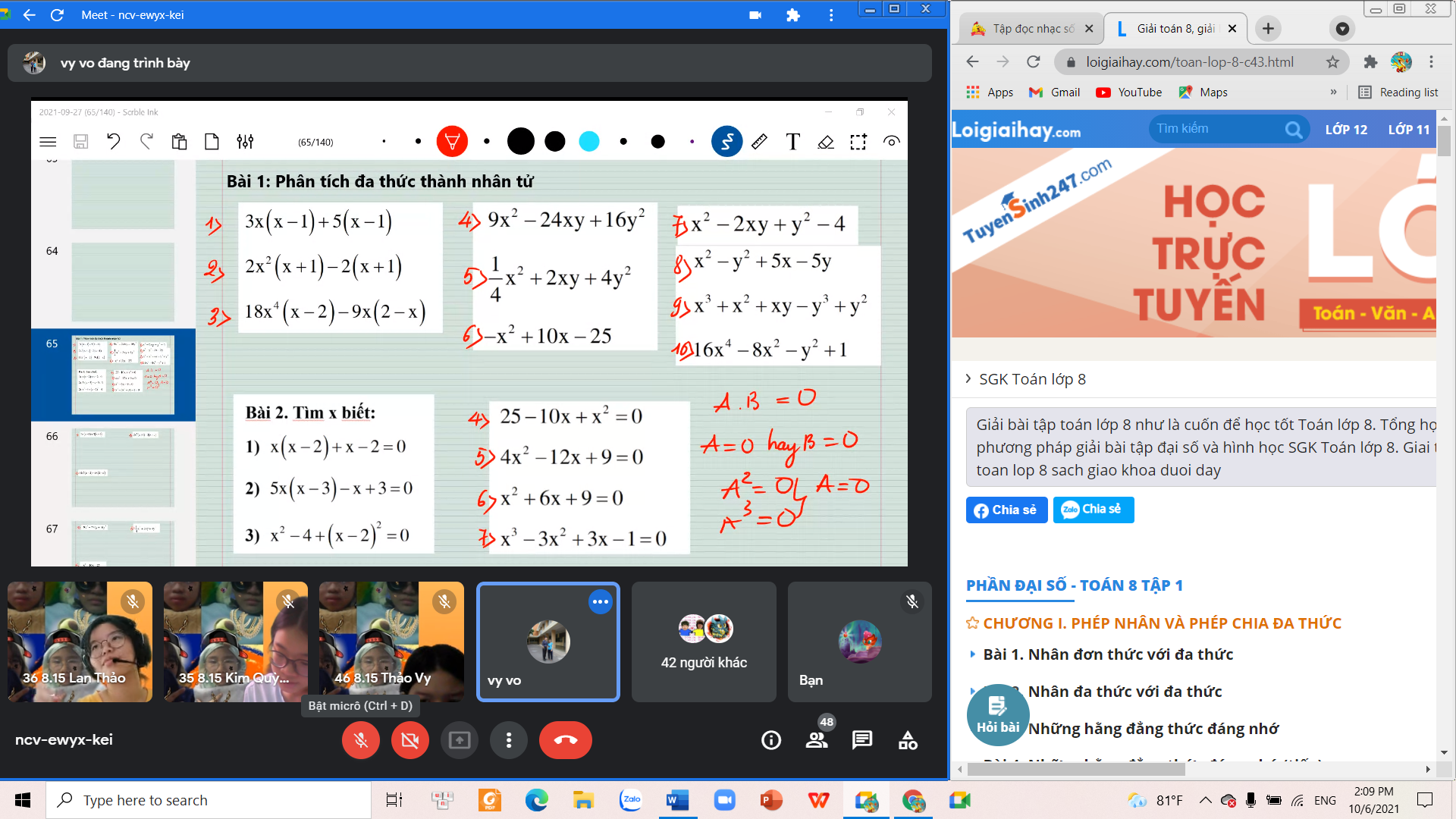


 bài 2 câu 1,2,3,5,9
bài 2 câu 1,2,3,5,9 




