K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2021
7.
\(\sqrt{4-x}\ge0\Rightarrow\sqrt{4-x}+\sqrt{3}\ge\sqrt{3}\) đáp án D
8.
\(y=x^2+\dfrac{1}{2x}+\dfrac{1}{2x}\ge3\sqrt[3]{\dfrac{x^2}{4x^2}}=\dfrac{3}{\sqrt[3]{4}}\)
Dấu "=" xảy ra khi \(x^2=\dfrac{1}{2x}\Leftrightarrow x=\dfrac{1}{\sqrt[3]{2}}\) đáp án D
9.
\(y\ge2\sqrt{\dfrac{2x}{x}}-\left(1+\sqrt{2}\right)^2=2\sqrt{2}-\left(3+2\sqrt{2}\right)=-3\) đáp án B
10.
\(y'=\dfrac{1-2x}{\left(x-2\right)^2\sqrt{x^2-1}}\Rightarrow\) hàm đồng biến trên \((-\infty;-1]\) và nghịch biến trên \(\left[1;\dfrac{3}{2}\right]\)
\(f\left(-1\right)=f\left(1\right)=0\) ; \(f\left(\dfrac{3}{2}\right)=-\sqrt{5}\)
\(\Rightarrow f\left(x\right)_{max}=0\) ; \(f\left(x\right)_{min}=-\sqrt{5}\) đáp án A
11.
\(f'\left(x\right)=\dfrac{5-x}{\left(x^2+2\right)\sqrt{x^2+5}}=0\Rightarrow x=5\) \(\Rightarrow f\left(5\right)=\dfrac{\sqrt{30}}{5}\)
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=1\) ; \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-1\)
Hàm đạt GTLN tại \(x=5\) và ko có GTNN, đáp án D
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
Xét \(I_1=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)cosxdx=2\int\limits^{\dfrac{\pi}{2}}_0f\left(sinx\right)d\left(sinx\right)\)
Đặt \(sinx=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=5-t\)
\(I_1=2\int\limits^1_0\left(5-t\right)dt=9\)
Xết \(I_2=3\int\limits^1_0f\left(3-2x\right)dx=-\dfrac{3}{2}\int\limits^1_0f\left(3-2x\right)d\left(3-2x\right)\)
Đặt \(3-2x=t\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(t\right)=t^2+3\)
\(I_2=-\dfrac{3}{2}\int\limits^1_3\left(t^2+3\right)dt=\dfrac{3}{2}\int\limits^3_1\left(t^2+3\right)dt=22\)
\(\Rightarrow I=9+22=31\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
Đặt \(f\left(x\right)=\dfrac{1}{3}x^3-x^2+mx+1\Rightarrow f'\left(x\right)=x^2-2x+m\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}x^2-2x+m\ge0;\forall x\ge1\\f\left(1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ge1\\m+\dfrac{1}{3}\ge0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
\(\Rightarrow m=\left\{1;2;3\right\}\)
HN
13 tháng 10 2021
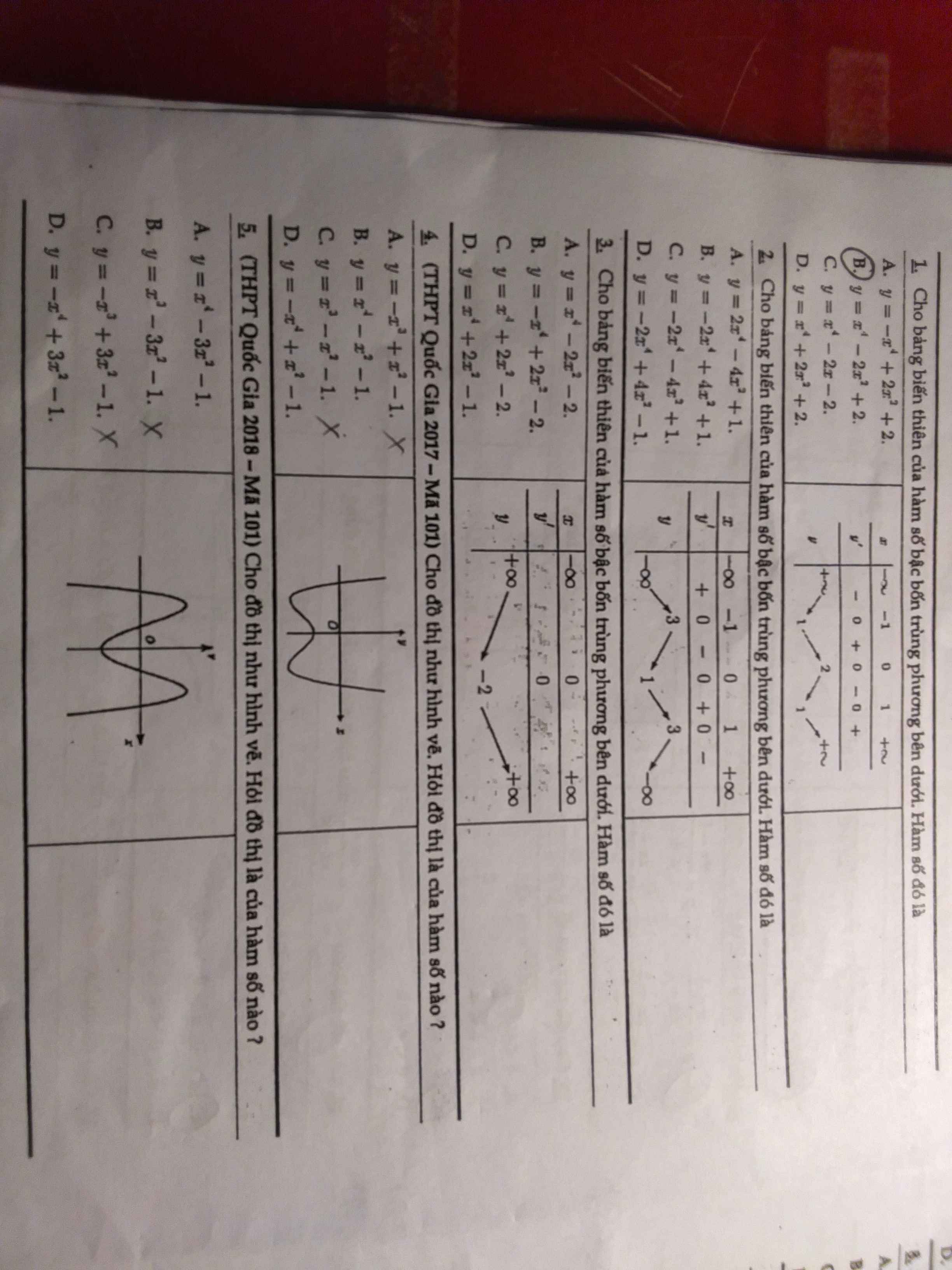
1. Chọn B.
2. Chọn B.
3. Chọn D.
4. Chọn B.
5. Chọn D.
6. Chọn A.
7. Chọn D.
8. Chọn A.
9. Chọn D.
10. Chọn C.
11. Chọn A.
12.Chọn B.
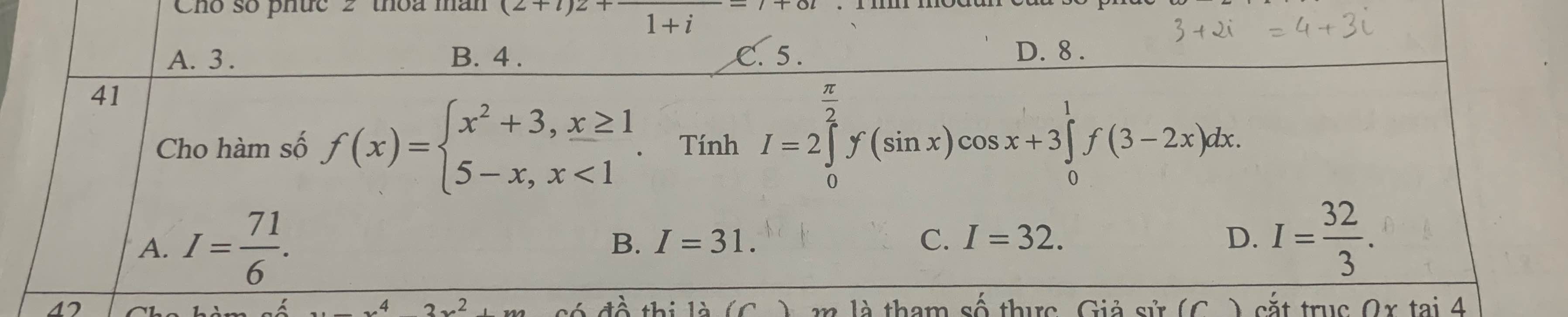
Bạn cập nhật lại đề lên nhé