Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

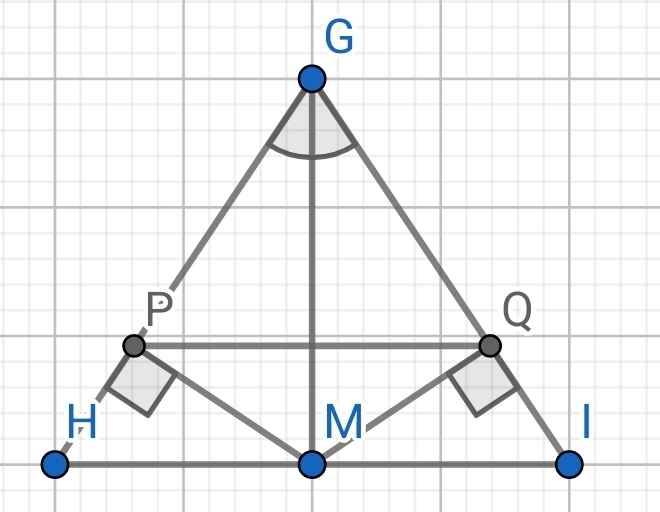 a) Do GM là tia phân giác của ∠HGI (gt)
a) Do GM là tia phân giác của ∠HGI (gt)
⇒ ∠HGM = ∠IGM
Xét ∆GHM và ∆GIM có:
GH = GI (do ∆GHI cân tại G)
∠HGM = ∠IGM (cmt)
GM là cạnh chung
⇒ ∆GHM = ∆GIM (c-g-c)
b) Do ∆GHM = ∆GIM (cmt)
⇒ HM = IM (hai cạnh tương ứng)
Do ∆GHM = ∆GIM (cmt)
⇒ ∠GMH = ∠GMI (hai góc tương ứng)
Mà ∠GMH + ∠GMI = 180⁰ (kề bù)
⇒ ∠GMH = ∠GMI = 180⁰ : 2 = 90⁰
⇒ GM ⊥ HI
c) Do ∠HGM = ∠IGM (cmt)
⇒ ∠PGM = ∠QGM
Xét hai tam giác vuông: ∆GMP và ∆GMQ có:
GM là cạnh chung
∠PGM = ∠QGM (cmt)
⇒ ∆GMP = ∆GMQ (cạnh huyền góc nhọn)
⇒ MP = MQ (hai cạnh tương ứng)
⇒ ∆MPQ cân tại M

a) Xét ΔABD và ΔACD có:
AD chung
góc ABD=góc ACD ( do AD là phân giác của góc BAC)
AB=AC ( ΔABC cân tại A)
Do đó:ΔABD=ΔACD (c-g-c) (đpcm)
Ta có:
AD vuông góc BC(tính chất Δ vuông)
EH vuông góc BC (theo đầu bài)
=>AD//EH (cùng vuông góc với BC)
=>góc ADE=góc DEH (2 góc so le trong)
Lại có:ΔDEC cân theo câu c:
=>góc EDC=góc ECD
mà góc ECD=góc ABD (ΔABC cân tại A)
=>góc EDC=góc ABD.
Xét ΔBAD có: góc ABD + góc BAD=90 độ (do ΔBAD vuông tại D)
và ΔDEH có: góc EDH + góc DEH =90 độ (do ΔDEH vuông tại H)
=> góc BAD=góc DEH
Mà góc BAD=góc DAE (AD là phân giác của góc A)
góc ADE=góc DEH (2 góc so le trong)
=>góc DAE=góc ADE
=>ΔAED cân tại E
=>DE=AE
mà DE=EC (ΔDEC cân tại E)
=>AE=EC
=>E là trung điểm của AC
=>3 điểm B,G,E thẳng hàng (đpcm)

Xét \(\Delta BHM\) và \(\Delta CMK\) có :
MH = MK (gt)
BM = CM (gt)
\(\widehat{HMB}=\widehat{KMC}\) (đối đỉnh)
\(\Rightarrow\Delta HMB=\Delta KMC\) (c . g . c)

a: Xét ΔMBH và ΔMCK có
MB=MC
góc BMH=góc CMK
MH=MK
Do đo:ΔMBH=ΔMCK
b: ΔMBH=ΔMCK
nên góc MBH=góc MCK
=>CK//BH
=>CK vuông góc với AC
c: Xet ΔCHG có
CI vừa là đường cao, vừa là trung tuyến
nên ΔCHG cân tại C
=>CH=CG=BK
a: Xét ΔGHM và ΔGIM có
GH=GI
\(\widehat{HGM}=\widehat{IGM}\)
GM chung
Do đó: ΔGHM=ΔGIM
b: Ta có: ΔGHM=ΔGIM
nên MH=MI
Ta có: ΔGHI cân tai G
mà GM là đường trung tuyến
nên GM là đường cao
c: Xét ΔGPM vuông tại P và ΔGQM vuông tại Q có
GM chung
\(\widehat{PGM}=\widehat{QGM}\)
Do đó: ΔGPM=ΔGQM
Suy ra: MP=MQ
hay ΔMPQ cân tại M