Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ `KI ⊥ BC(I in BC)`
Đặt `BG` là p/g của góc ngoài tại `hat(ABC)`
`CH` là p/g của góc ngoài tại `hat(ACB)`
+, Có : `BG` là p/g của góc ngoài tại `hat(ABC)`
`=>hat(B_1)=hat(B_2)`
mà `hat(B_1)=hat(B_3);hat(B_2)=hat(B_4)` ( đối đỉnh )
nên `hat(B_3)=hat(B_4)`
+, Có : `CH` là p/g của góc ngoài tại `hat(ACB)`
`=>hat(C_1)=hat(C_2)`
mà `hat(C_1)=hat(C_3);hat(C_2)=hat(C_4)` ( đối đỉnh )
nên `hat(C_3)=hat(C_4)`
Xét `Delta BEK` và `Delta BIK` có :
`{:(hat(F)=hat(I_1)(=90^0)),(KB-chung),(hat(B_3)=hat(B_4)(cmt)):}}`
`=>Delta BEK=Delta BIK(c.h-g.n)`
`=>KE=KI` ( 2 cạnh t/ứng ) (1)
Xét `Delta KIC` và `Delta KEC` có :
`{:(hat(I_2)=hat(E)(=90^0)),(KC-xhung),(hat(C_3)=hat(C_4)(cmt)):}}`
`=>Delta KIC=Delta KEC(c.h-g.n)`
`=> KI=KE` ( 2 cạnh t/ứng ) (2)
Từ (1) và (2) `=>KF=KE(=KI)(đpcm)`

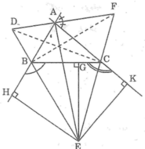
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.