K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
V
0
GH
12 tháng 7 2023
1
Với \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\)
\(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\left(\dfrac{x^2+2x+1}{4x^4-4x^2+1}\right)\\ =\left(\dfrac{\left(x-1\right)\left(x+1\right)}{\left(2-x\right)\left(x+1\right)}+\dfrac{x^2}{\left(x+1\right)\left(2-x\right)}\right)\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{x^2-1+x^2}{\left(x+1\right)\left(2-x\right)}\left(\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\right)\\ =\dfrac{\left(2x^2-1\right)\left(x+1\right)^2}{\left(x+1\right)\left(2-x\right)\left(2x^2-1\right)^2}\\ =\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}\)
2
Để M = 0 thì \(\dfrac{x+1}{\left(2-x\right)\left(2x^2-1\right)}=0\Rightarrow x+1=0\Rightarrow x=-1\) (loại)
Vậy không có giá trị x thỏa mãn M = 0
H9
HT.Phong (9A5)
CTVHS
12 tháng 7 2023
1) \(M=\left(\dfrac{x-1}{2-x}-\dfrac{x^2}{x^2-x-2}\right)\cdot\dfrac{x^2+2x+1}{4x^4-4x^2+1}\) (ĐK: \(\left\{{}\begin{matrix}x\ne2\\x\ne-1\\x\ne\sqrt{\dfrac{1}{2}}\end{matrix}\right.\))
\(M=\left(\dfrac{-\left(x-1\right)}{x-2}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}-\dfrac{x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-\left(x^2-1\right)-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\left(\dfrac{-x^2+1-x^2}{\left(x-2\right)\left(x+1\right)}\right)\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-2x^2+1}{\left(x-2\right)\left(x+1\right)}\cdot\dfrac{\left(x+1\right)^2}{\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(2x^2-1\right)\left(x+1\right)^2}{\left(x-2\right)\left(x+1\right)\left(2x^2-1\right)^2}\)
\(M=\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}\)
2) Ta có: \(M=0\)
\(\Rightarrow\dfrac{-\left(x+1\right)}{\left(x-2\right)\left(2x^2-1\right)}=0\)
\(\Leftrightarrow-\left(x+1\right)=0\)
\(\Leftrightarrow-x=1\)
\(\Leftrightarrow x=-1\left(ktm\right)\)
NN
1
17 tháng 1 2023
11)
\(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^{2^{ }}-4}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{x^2-2^2}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{2x}{x+2}\) \(\times\) \(\dfrac{\left(x-2\right)\left(x+2\right)}{4}\) - \(\dfrac{x}{2}\)
= \(\dfrac{x\left(x-3\right)}{2}\)
N
0
26 tháng 7 2021
19. 3x2-4x+1
= 3x2-3x-x+1
= (3x2-3x)-(x-1)
= 3x(x-1)-(x-1)
= (3x-1)(x-1)
20.3x2+4x-7
= 3x2+3x-7x-7
= (3x2+3x)-(7x+7)
= 3x(x+1)-7(x-1)
= (3x-7)(x-1)
21.3x2+7x-6
= 3x2+9x-2x-6
= (3x2+9x)-(2x+6)
= 3x(x+3)-2(x+3)
= (3x-2)(x+3)
22.3x2+3x-6
= 3x2+6x-3x-6
=(3x2+6x)-(3x+6)
= 3x(x+2)-3(x+2)
=(3x-3)(x+2)
= 3(x-1)(x+2)
23. 3x2-3x-6
=(3x2-6x)+(3x-6)
=3x(x-2)+3(x-2)
=(3x+3)(x-2)
= 3(x+1)(x-2)
24.6x2-13x+6
= 6x2-9x-4x+6
= (6x2-9x)-(4x-6)
=3x(2x-3)-2(2x-3)
=(3x-2)(2x-3)
25.6x2+13x+6
= 6x2+9x+4x+6
= (6x2+9x)+(4x+6)
=3x(2x+3)+2(2x+3)
=(3x+2)(2x+3)
26. 6x2+15x+6
= (6x2+12x)+(3x+6)
= 6x(x+2)+3(x+2)
=(6x+3)(x+2)
=3(2x+1)(x+2)
27. 6x2-15x+6
= (6x2-12x)-(3x-6)
= 6x(x-2)-3(x-2)
=(6x-3)(x-2)
=3(2x-1)(x-2)
28. 6x2+20x+6
= (6x2+18x)+(2x+6)
= 6x(x+3)+2(x+3)
= (6x+2)(x+3)
= 2(3x+1)(x+3)
29.6x2-20x+6
= (6x2-18x)-(2x-6)
= 6x(x-3)+2(x-3)
= (6x-2)(x-3)
= 2(3x-1)(x-3)
30.6x2+12x+6
= (6x2+6x)+(6x+6)
= 6x(x+1)+6(x+1)
= (6x+6)(x+1)
= 6(x+1)(x+1)
= 6(x+1)2
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
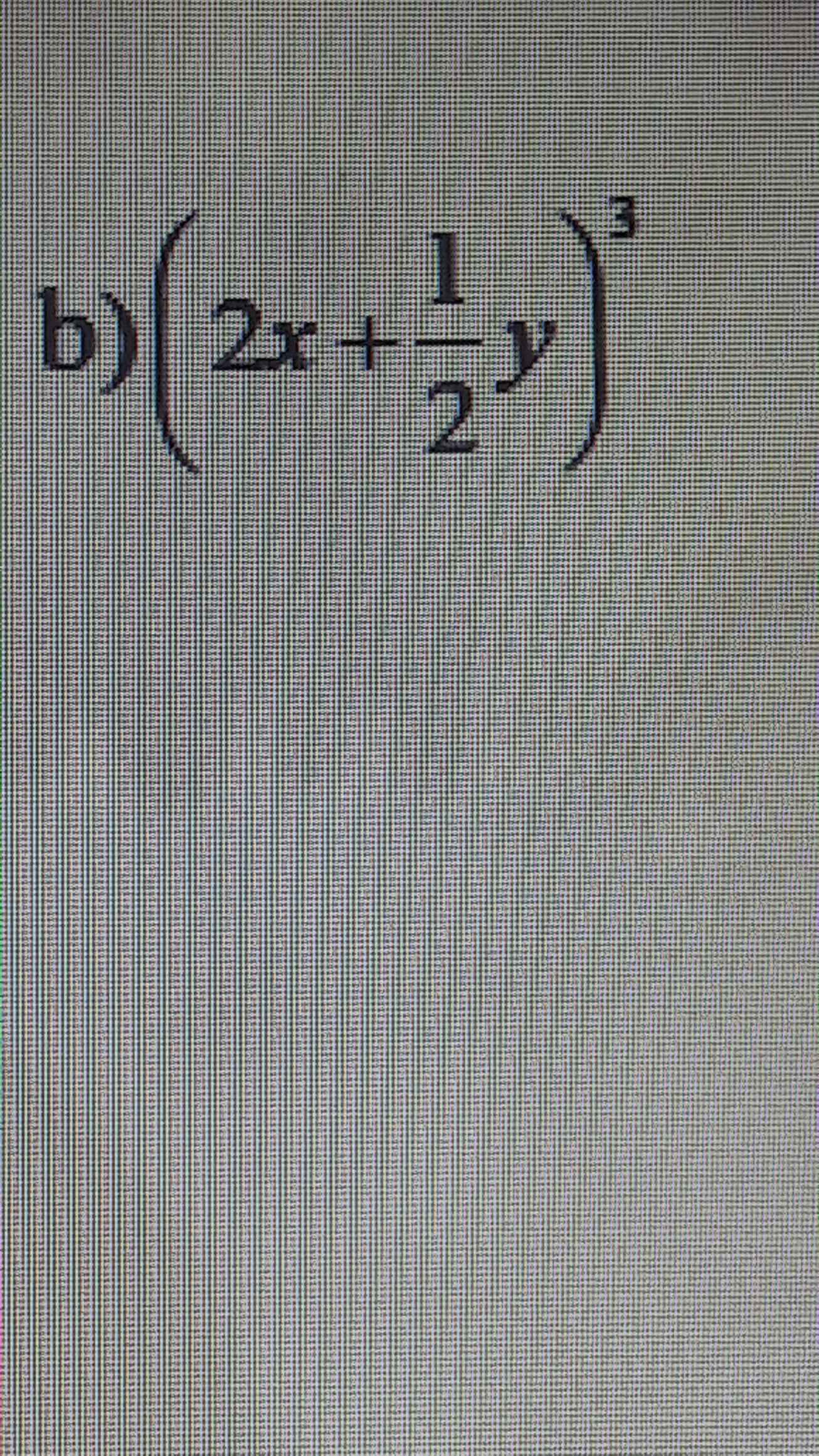
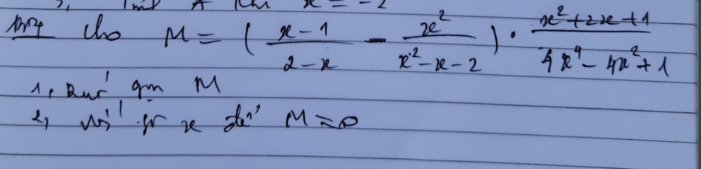
\(\left(2x+\dfrac{1}{2}y\right)^3=\left(2x\right)^3+3.\left(2x\right)^2.\dfrac{1}{2}y+3.2x.\left(\dfrac{1}{2}y\right)^2+\left(\dfrac{1}{2}\right)^3=8x^3+6x^2y+\dfrac{3}{2}xy^2+\dfrac{1}{8}y^3\)