Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, kẻ CE vuông góc với BA và song song với AD. => CE cũng vuông góc với CD.
Mà BA song song với CD (vì là hình thang) ; và CE cùng AD đều vuông góc với BA và CD ( là hình thang vuông ) nên CE = AD
S tam giác ABC=1/2.CE.BA
S tam giác ADC=1/2.CD.AD
Mà CE=AD; BA = 1/3 CD => S abc = 1/3 S adc
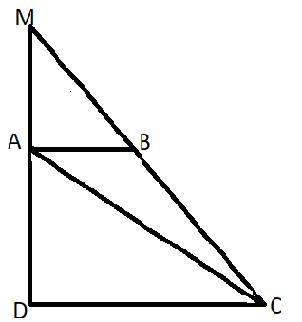
Cho hình thang vuông ABCD , vuông ở A và D , đáy AB bằng 1/3 đáy CD . Kéo dài DA và CB cắt nhau tại M . a) So sánh diện tích tam giác ABM và diện tích tam giác ACM . b) Tính diện tích hình thang ABCD , biết rằng diện tích tam giác ABM bằng 40 cm vuông .

Gọi 4 số đó lần lượt là : a ; a + 1 ; a + 2 ; a + 3
tổng là:
a + a + 1 + a + 2 + a + 3 = 4a +6 = 4a + 4 + 2 = 4 ( a + 1) + 2
không chia hết cho 4
=> ĐPCM
Bài 1: gọi số 4 tự nhiên liên tiếp là: n, n+1, n+2, n+3
Ta có : n+n+1+n+2+n+3 ==> 4n+6
do 4n chia hết cho 4 mà 6 ko chia hết cho 4
==> 4n+6 ko chia hết cho 4
Vậy tổng 4 số tự nhiên liên tiếp ko chia hết cho 4

a) Ta có: S hình thang ABCD là : \(\frac{\left(AB+CD\right)\cdot h}{2}=450\Rightarrow3CD\cdot h=900\Rightarrow h=\frac{900}{3CD}=\frac{300}{CD}\)
Mà hình thang ABCD và tam giác ABC có cùng đường cao hạ từ C
Nên diện tích tam giác ABC là: \(\frac{AB\cdot h}{2}=\frac{2CD\cdot h}{2}=\frac{2CD\cdot\frac{300}{CD}}{2}=300\left(cm^2\right)\)
b) hình tứ giác có diện tích nhỏ nhất là hình thang CMAN (vì CM=CD/2 và AN=AB/2)
Diện tích tứ giác đó là: \(\frac{\left(CM+AN\right)\cdot h}{2}=\frac{1,5CD\cdot\frac{300}{CD}}{2}=225\left(cm^2\right)\)
c)IM<IN (sr nha mình bận một chút)
có gì k cho mình nha
a: Vì AB=1/3CD
nên \(\dfrac{S_{ABC}}{S_{ADC}}=\dfrac{AB}{DC}=\dfrac{1}{3}\)
=>\(S_{ABC}=\dfrac{S_{ADC}}{3}\)
b: Xét ΔMDC có AB//DC
nên ΔMAB~ΔMDC
=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{AB}{DC}\right)^2=\dfrac{1}{9}\)
=>\(\dfrac{S_{MAB}}{S_{ABCD}}=\dfrac{1}{8}\)
=>\(S_{MAB}=\dfrac{84}{8}=10.5\left(cm^2\right)\)