
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi số sp mỗi ngày phân xưởng đó sản xuất được theo dự định là a (sản phẩm) (a: nguyên, dương)
Vậy số ngày sản xuất dự kiến là: 1100/a (ngày)
Vì vượt mức 5sp/1 ngày nên số ngày sản xuất thực tế là: 1100/(a+5) (ngày)
Vì phân xưởng làm hoàn thành sớm hơn 2 ngày, nên ta có pt:
\(\dfrac{1100}{a}=\dfrac{1100}{a+5}+2\left(a\ne0;a\ne-5\right)\\ \Leftrightarrow\dfrac{1100\left(a+5\right)}{a\left(a+5\right)}=\dfrac{1100a+2a\left(a+5\right)}{a\left(a+5\right)}\\ \Leftrightarrow2a^2+10a-5500=0\\ \Leftrightarrow2a^2-100a+110a-5500=0\\ \Leftrightarrow2a\left(a-50\right)+110\left(a-50\right)=0\\ \Leftrightarrow\left(2a+110\right)\left(a-50\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2a+110=0\\a-50=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-55\left(loại\right)\\a=50\left(Nhận\right)\end{matrix}\right.\)
Vậy theo kế hoạch, mỗi ngày phân xưởng phải sx được 50 sản phẩm




\(B=\sqrt{14+2\sqrt{10}+2\sqrt{14}+2\sqrt{35}}\)
\(=\sqrt{2}+\sqrt{5}+\sqrt{7}\)

b: Xét \(\left(O\right)\) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét \(\left(O\right)\) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: OM=OA
nên O nằm trên đường trực của MA\(\left(1\right)\)
Ta có: CA=CM
nên C nằm trên đường trực của MA\(\left(2\right)\)
Ta có: OM=OB
nên O nằm trên đường trực của MB\(\left(3\right)\)
Ta có: DM=DB
nên D nằm trên đường trực của MB\(\left(4\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra OC là đường trung trực của MA
hay OC\(\perp\)MA tại E
Từ \(\left(3\right),\left(4\right)\) suy ra OD là đường trung trực của MB
hay OD\(\perp\)MB tại F
Xét tứ giác MEOF có
\(\widehat{MEO}=\widehat{EMF}=\widehat{MFO}=90^0\)
Do đó: MEOF là hình chữ nhật

983495438158134591856457654735756725124124+95718934578147058714385713758147597389454+8739715735617923445:138702347123895135897134895714375934:0=0!
vì số nào chia cho 0 cũng bằng 0!
mình cần 1s nha

Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)
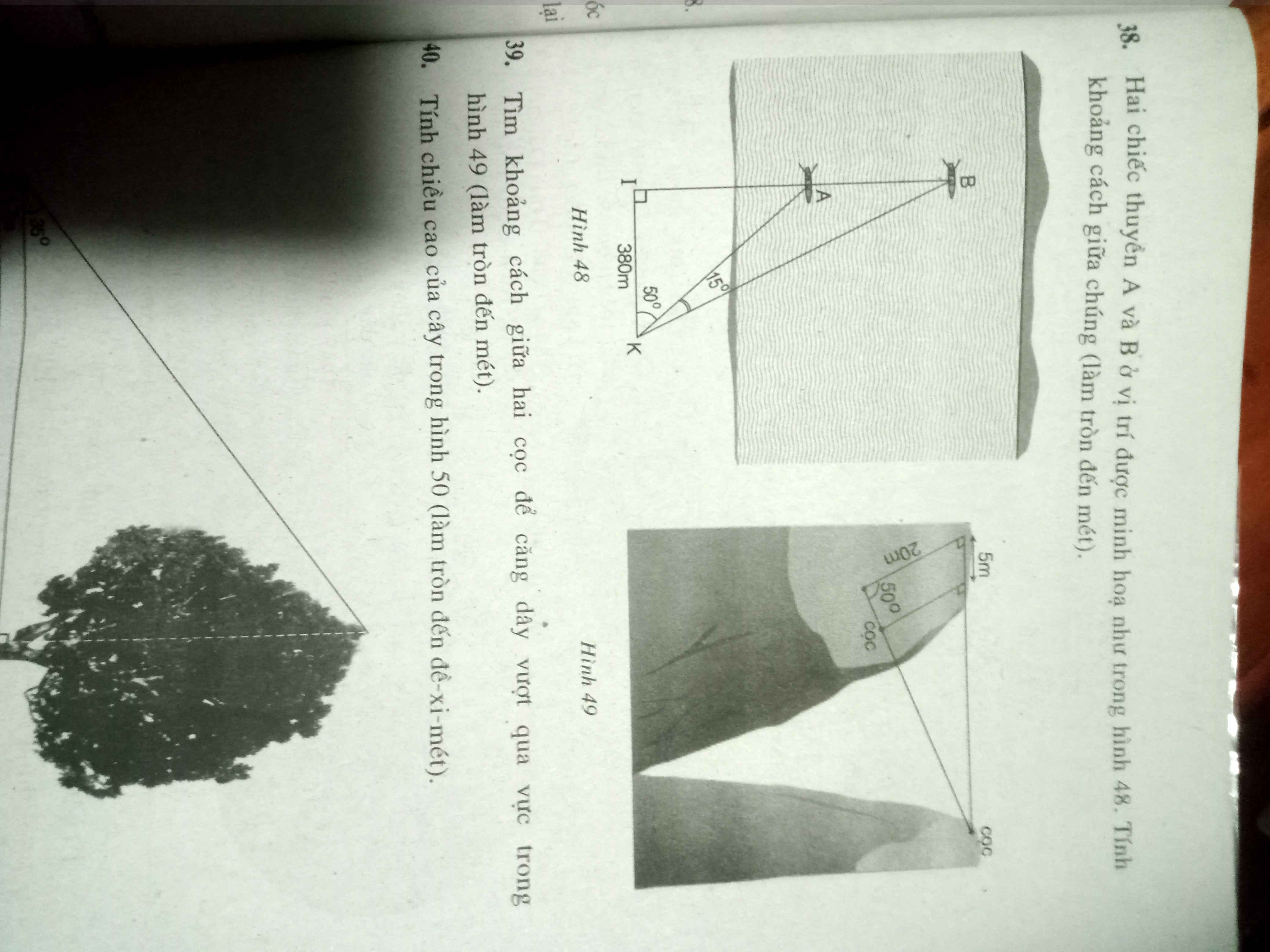
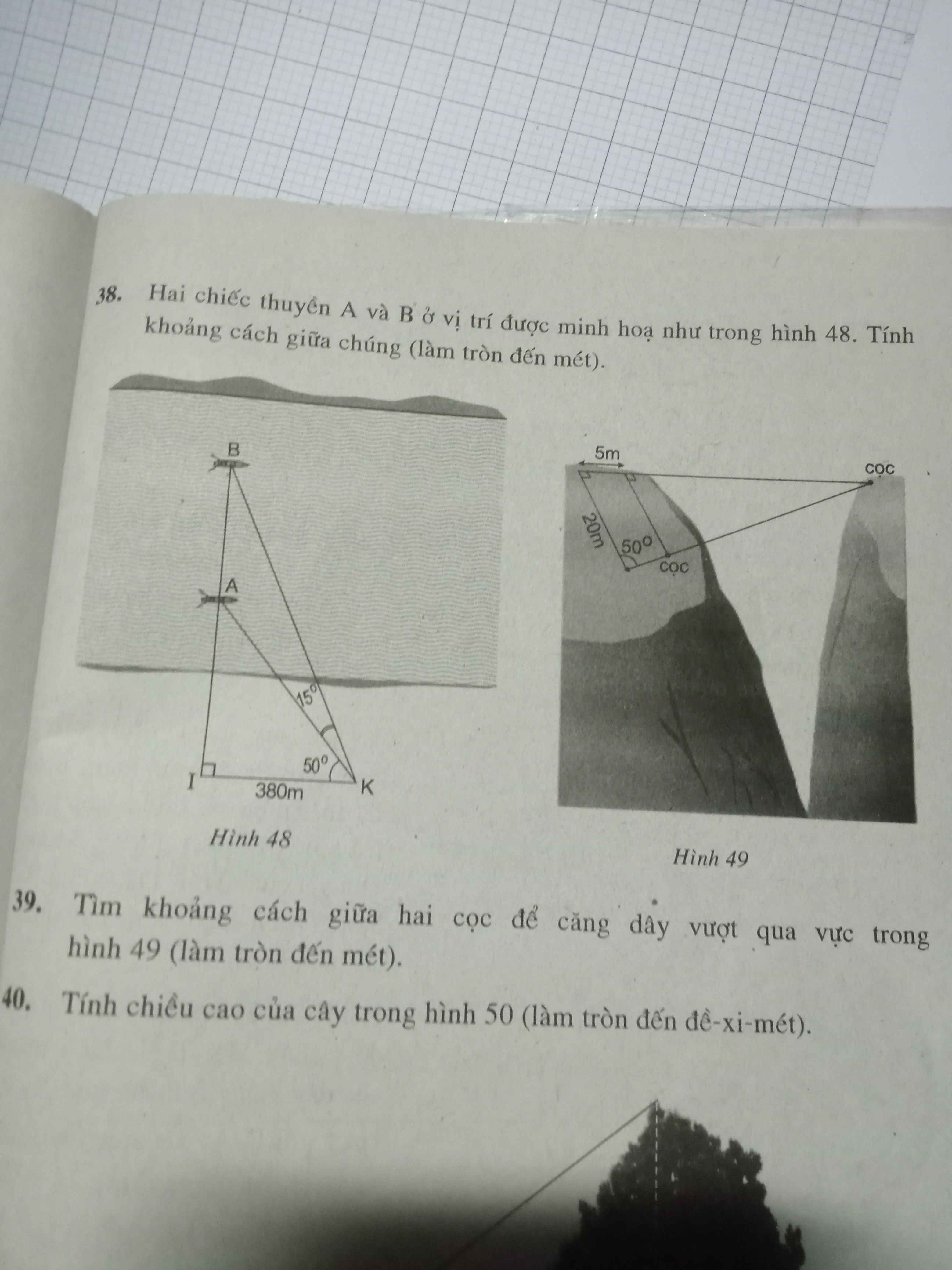



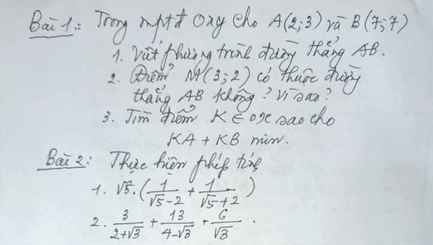 làm hộ mik bài 1 thôi nha
làm hộ mik bài 1 thôi nha

