
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) Ta có: \(\left(3x-5\right)\left(2x+1\right)=12\)
\(\Leftrightarrow6x^2+3x-10x-5-12=0\)
\(\Leftrightarrow6x^2-7x-17=0\)
\(\Delta=\left(-7\right)^2-4\cdot6\cdot\left(-17\right)=49+408=457\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{7+\sqrt{457}}{12}\\x_2=\dfrac{7-\sqrt{457}}{12}\end{matrix}\right.\)


Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{3}}=\dfrac{b}{\dfrac{1}{4}}=\dfrac{c}{\dfrac{1}{5}}=\dfrac{a+b+c}{\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}}=\dfrac{94}{\dfrac{47}{60}}=120\)
Do đó: a=40; b=30; c=24

17: A=M*N
=25a^3b*8a^2b^3=200a^5b^4
M và N cùng dấu
=>M*N>0
=>200*a^5*b^4>0
=>a^5>0
=>a>0

M=-25a3b=a2b.(-25a). N=8a2b3=a2b.(8b2).
Do M và N cùng dấu nên -25a và 8b2 cùng dấu, mà 8b2\(\ge\)0 nên a\(\ge\)0.

Bài 1:
\(a,A=x^2y^3-\dfrac{5}{4}\cdot\dfrac{4}{5}x^2y^3=x^2y^3-x^2y^3=0\\ b,B=\dfrac{1}{2}a^3b^2-\dfrac{2}{3}a^3b^2=-\dfrac{1}{6}a^3b^2\)
Bài 2:
\(A=-3x^3y^3z-5x^3y^3z=-8x^3y^3z\)
Bài 3:
\(=-3x^2y^2+4x^2y^2=x^2y^2\)
Vì \(x^2\ge0;y^2\ge0\Leftrightarrow x^2y^2\ge0\left(đpcm\right)\)

Bài 3:
b: \(10^6-5^7=5^6\left(2^6-5\right)=5^6\cdot59⋮59\)


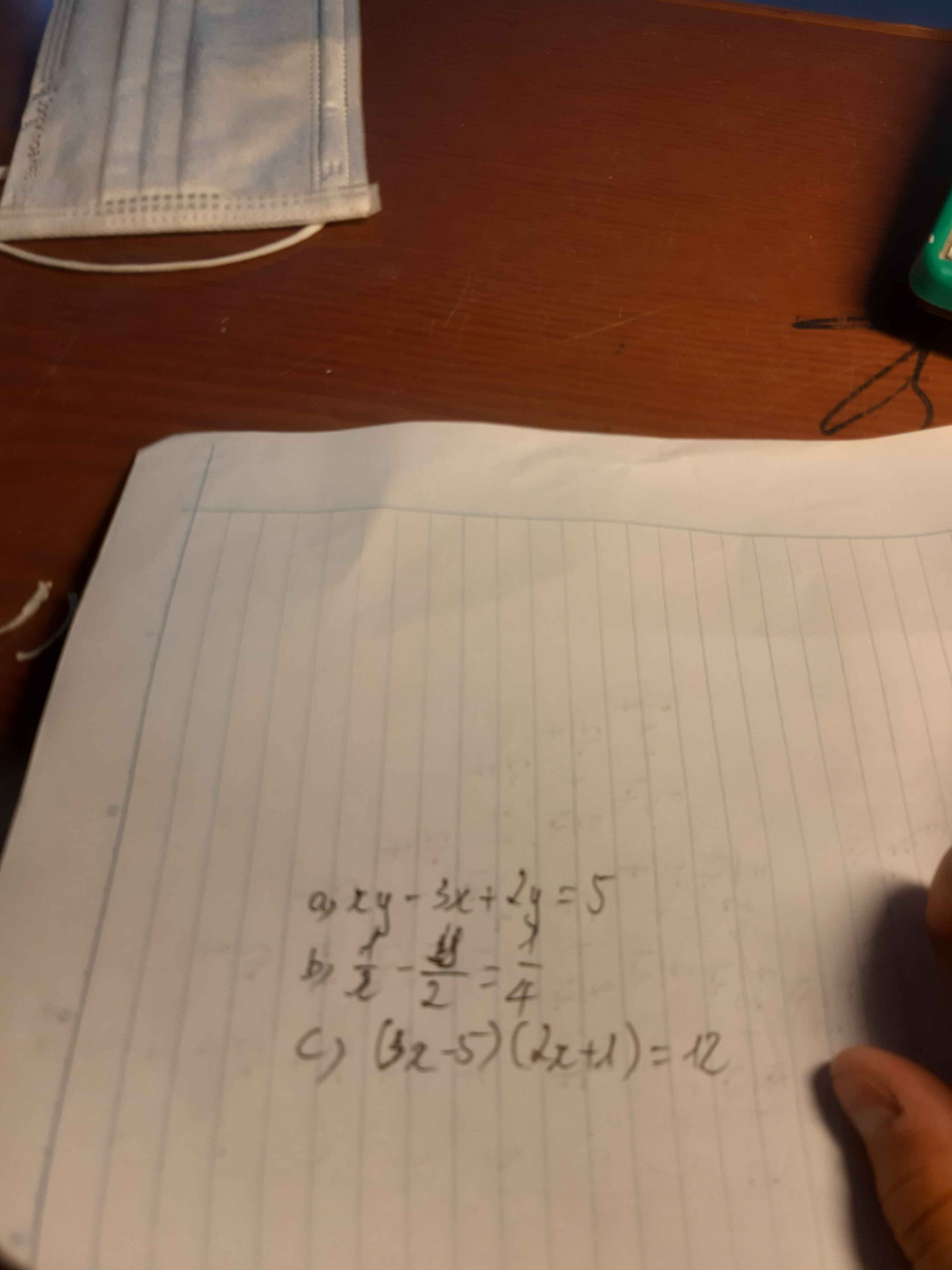



 Giải giúp em câu cuối cùng cố gắng nhìn giúp ạ tại kêu bạn chụp giúp.Giải giúp mai em thi rồi
Giải giúp em câu cuối cùng cố gắng nhìn giúp ạ tại kêu bạn chụp giúp.Giải giúp mai em thi rồi



tách ra bn ơi
tách ra