K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
Từ đề bài ta suy ra tất cả các mặt bên của hộp đều là hình thoi (được ghép từ 2 tam giác đều)
\(\Rightarrow A'D=A'B=A'A=a\Rightarrow\) hình chiếu vuông góc của A' lên (ABCD) trùng trọng tâm E của tam giác ABD
\(\widehat{DBE}=\dfrac{1}{2}.60^0=30^0\Rightarrow\widehat{CBE}=\widehat{CBD}+\widehat{DBE}=60^0+30^0=90^0\)
\(\Rightarrow BC\perp BE\)
Mà \(A'E\perp\left(ABCD\right)\Rightarrow A'E\perp BC\)
\(\Rightarrow BC\perp\left(A'BE\right)\Rightarrow BC\perp A'B\)
\(\Rightarrow B'C'\perp A'B\)
\(AE=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'E=\sqrt{A'A^2-AE^2}=\dfrac{a\sqrt{6}}{3}\)
Qua C' dựng đường thẳng song song A'E cắt AC tại F \(\Rightarrow C'F=A'E=\dfrac{a\sqrt{6}}{3}\)
\(CF=AE=\dfrac{a\sqrt{3}}{3}\) ; \(AC=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\Rightarrow AF=AC+CF=\dfrac{4a\sqrt{3}}{3}\)
\(\Rightarrow AC'=\sqrt{AF^2+C'F^2}=a\sqrt{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
\(CP=\dfrac{1}{3}CC'\) ; \(CN=\dfrac{1}{3}BC\)
Nối PN kéo dài cắt BB' tại J
Talet: \(\dfrac{CP}{BJ}=\dfrac{CN}{NB}=\dfrac{1}{2}\Rightarrow BJ=2CP=\dfrac{2a}{3}\Rightarrow\dfrac{BJ}{B'J}=\dfrac{\dfrac{2a}{3}}{a+\dfrac{2a}{3}}=\dfrac{2}{5}\)
Nối JM cắt A'B' kéo dài tại K
Talet: \(\dfrac{BM}{B'K}=\dfrac{BJ}{B'J}=\dfrac{2}{5}\Rightarrow B'K=\dfrac{5BM}{2}=\dfrac{5a}{4}\)
Nối MN cắt BD tại H và cắt CD tại G
Talet: \(\dfrac{CG}{BM}=\dfrac{CN}{BN}=\dfrac{1}{2}\Rightarrow CG=\dfrac{1}{2}BM=\dfrac{a}{4}\Rightarrow DG=a+\dfrac{a}{4}=\dfrac{5a}{4}\)
Talet: \(\dfrac{BH}{DH}=\dfrac{BM}{DG}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (1)
Nối GP cắt C'D' tại Q
Talet: \(\dfrac{CG}{C'Q}=\dfrac{CP}{C'P}=\dfrac{1}{2}\Rightarrow C'Q=2CG=\dfrac{a}{2}\)
Nối QK cắt B'D' tại L
Talet: \(\dfrac{D'L}{B'L}=\dfrac{D'Q}{B'K}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (2)
(1);(2) \(\Rightarrow D'L=BH\) (do \(BD=B'D'\))
Nối HL cắt BD' tại I
Talet: \(\dfrac{D'I}{IB}=\dfrac{D'L}{BH}=1\)
Gọi F là giao điểm QK và A'D', O là giao điểm JK và A'A
Ta đồng thời suy ra luôn NPQFOM là thiết diện của (MNP) và chóp
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 2 2022
Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)
Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 2 2022
Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):
Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)
\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)
Do đó:
\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
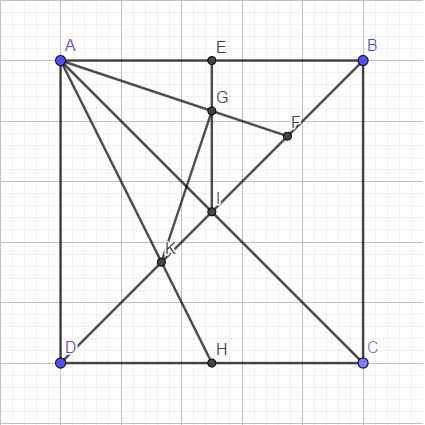
Đặt tên điểm như hình vẽ bên dưới
Ta có: F là trung điểm BI \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AF}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)=\dfrac{1}{3}\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\)
\(\overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AH}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\)
\(\overrightarrow{GK}=\overrightarrow{GA}+\overrightarrow{AK}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AG}.\overrightarrow{GK}=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)=-\dfrac{1}{12}AB^2+\dfrac{1}{12}AD^2=0\)
\(\Rightarrow AG\perp GK\)
\(\left\{{}\begin{matrix}\overrightarrow{GA}=\left(a+\dfrac{1}{3};b\right)\\\overrightarrow{KG}=\left(0;\dfrac{5}{3}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{GA}.\overrightarrow{KG}=\left(a+\dfrac{1}{3}\right).0+\dfrac{5}{3}b=0\Rightarrow b=0\)
Mặt khác: \(AG^2-GK^2=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)^2-\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)^2=0\)
\(\Rightarrow AG^2=GK^2\Rightarrow\left(a+\dfrac{1}{3}\right)^2=\left(\dfrac{5}{3}\right)^2\Rightarrow a=-2\)
giup em b c hinh voi a mai em thi roi
12 tháng 5 2023
2:
a: BC vuông góc SA
BC vuông góc AB
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)
BD vuông góc SA
BD vuông góc AC
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: (SC;(ABCD))=(CS;CA)=góc SCA
\(AC=\sqrt{AB^2+BC^2}=2a\sqrt{2}\)
tan SCA=SA/AC=căn 3/2*căn 2
=>góc SCA=31 độ
(SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=căn 3/2
=>góc SDA=41 độ
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
ĐKXĐ cho căn thức: \(x\ge-\dfrac{1}{2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{3x+1-\sqrt{2x+1}}{x^2-x}=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{3}{x}+\dfrac{1}{x^2}-\sqrt{\dfrac{2}{x^3}+\dfrac{1}{x^4}}}{1-\dfrac{1}{x}}=\dfrac{0}{1}=0\)
\(\Rightarrow y=0\) là TCN
\(\lim\limits_{x\rightarrow0}\dfrac{3x+1-\sqrt{2x+1}}{x^2-x}=\lim\limits_{x\rightarrow0}\dfrac{9x^2+4x}{x\left(x-1\right)\left(3x+1+\sqrt{2x+1}\right)}=\lim\limits_{x\rightarrow0}\dfrac{9x+4}{\left(x-1\right)\left(3x+1+\sqrt{2x+1}\right)}\)
\(=\dfrac{4}{-1\left(1+1\right)}\) hữu hạn
\(\Rightarrow x=0\) không phải tiệm cận
\(\lim\limits_{x\rightarrow1}\dfrac{3x+1-\sqrt{2x+1}}{x\left(x-1\right)}=\dfrac{4-\sqrt{3}}{0}=+\infty\Rightarrow x=1\) là TCĐ
Đồ thị hàm số có 2 tiệm cận
15 tháng 9 2017
dùng ông thức hạ bậc
cos2a=\(\dfrac{1+cos2a}{2}\)
pt<=>1+cos(4x+\(\dfrac{2\Pi}{3}\))-3sin(2x+\(\dfrac{5\Pi}{6}\))+1=0
<=>-\(\dfrac{1}{2}\)cos4x-\(\dfrac{\sqrt{3}}{2}\)sin4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x-\(\dfrac{3}{2}\)cos2x+2=0
<=>(-\(\dfrac{1}{2}\)cos4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)+(-\(\sqrt{3}\)sin2x.cos2x-\(\dfrac{3}{2}\)cos2x)=0
<=>[-\(\dfrac{1}{2}\)(1-2sin22x)+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0
<=>(sin22x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+\(\dfrac{3}{2}\))-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0
<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x+\(\sqrt{3}\))-cos2x.(sin2x+\(\dfrac{\sqrt{3}}{2}\))=0
<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x-cos2x+\(\sqrt{3}\))=0
tới đây bạn tự giải nhé
HP
6 tháng 9 2021
Đặt \(y=sinx\left(y\in\left[-1;1\right]\right)\).
\(cos\left(sinx\right)=1\)
\(\Leftrightarrow cosy=1\)
\(\Leftrightarrow y=k2\pi\)
Vì \(y\in\left[-1;1\right]\Rightarrow-1\le k2\pi\le1\Leftrightarrow-\dfrac{1}{2\pi}\le k\le\dfrac{1}{2\pi}\)
\(\Rightarrow k=0\)
\(\Rightarrow y=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
\(\Leftrightarrow k\in\left\{0;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\pi\\x=2\pi\end{matrix}\right.\)
\(\Rightarrow S=3\pi\)
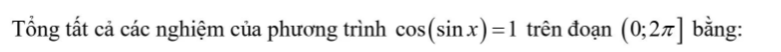
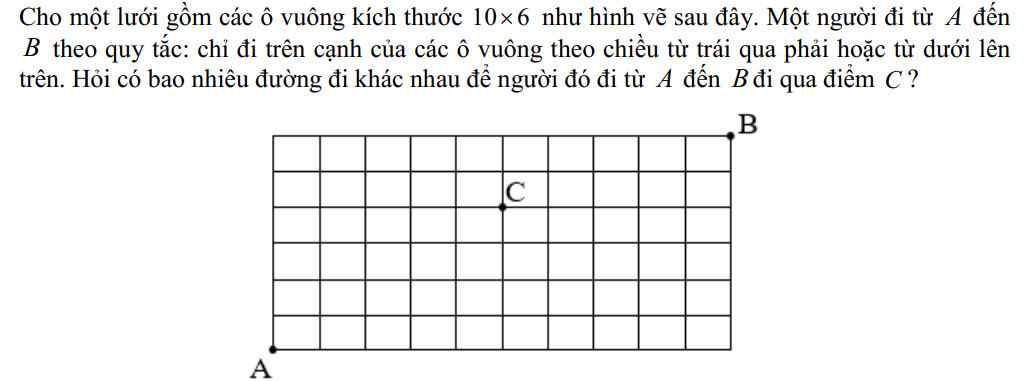
Từ A đến C, có 4 đoạn đi lên (nằm song song nhau) và 5 đoạn đi ngang nằm song song
Ta kí hiệu đi lên là L và đi ngang là N, như vậy, số cách đi từ A đến C là số cách sắp xếp 9 kí tự bao gồm 4L và 5N
\(\Rightarrow\) Có \(\dfrac{9!}{5!.4!}\) cách
Tương tự, từ C đến B có 2L và 5N, có \(\dfrac{7!}{2!.5!}\) cách
Tổng cộng: \(\dfrac{9!}{5!.4!}.\dfrac{7!}{2!.5!}\) cách đi từ A đến B
em cảm ơn thầyyyyyyyy