
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ta có: ADHE là hình chữ nhật
=>AH=DE(1)
Ta có: ΔAHM vuông tại H
=>AH<AM(2)
Từ (1) và (2) suy ra DE<AM
c: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nênMA=MC
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
Ta có: AEHD là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{B}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{B}\)
Ta có: \(\widehat{AED}+\widehat{MAC}\)
\(=\widehat{B}+\widehat{C}=90^0\)
=>DE\(\perp\)AM
d:Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường trung tuyến ứng với cạnh BC
=>H trùng với M
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc DAE
Xét hình chữ nhật ADHE có AH là phân giác của góc DAE
nên ADHE là hình vuông
=>Chu vi là \(C=3\cdot4=12cm\) và diện tích \(S=3^2=9\left(cm^2\right)\)

a) \(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\left(Đk:x\ne3\right)\)
\(A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}=x-y\)
b) \(\dfrac{5x}{x+1}=\dfrac{Ax\left(x-1\right)}{\left(1-x\right)\left(x+1\right)}\left(Đk:x\ne\pm1\right)\)
\(A=\dfrac{5x\left(1-x\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-5\)
c) \(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\left(Đk:x\ne-3;A\ne0\right)\)
\(A=\dfrac{\left(4x^2-5x+1\right)\left(x+3\right)}{4x-1}=\dfrac{\left(x-1\right)\left(4x-1\right)\left(x+3\right)}{4x-1}\)
\(=\left(x-1\right)\left(x+3\right)=x^2+2x-3\)

a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)


\(AC=2BM=20\left(cm\right)\)
\(\Rightarrow BC=\sqrt{AC^2-AB^2}=\sqrt{20^2-16^2}=12\left(cm\right)\)


\(\dfrac{x-3}{3}=4-\dfrac{1-2x}{5}\)
=>5(x-3)=60-3(1-2x)
=>5x-15=60-3+6x
=>5x-15=6x+57
=>6x+57=5x-15
hay x=-72(nhận)

bài 2:
a. <=> x2 +5x-3x-15<x2-12
<=> x2-x2+5x-3x<-12+15
<=>2x<3
<=>x<\(\dfrac{3}{2}\)
S={x|x<\(\dfrac{3}{2}\)}
b. <=> 9(x-4) - 3(2x-5) < 2(5x+7)
<=> 9x-36 -6x+15 < 10x+14
<=>9x-6x-10x<14+36-15
<=> -7x<35
<=>x>-5
S={x|x>-5}
bài 3:
gọi chiều rộng ban đầu là x
chiều dài ban đầu là 3x
gọi chiều rộng lúc sau là x+6
chiều dài lúc sau là 3x-5
theo đề ta có:
x.3x +334= (x+6)(3x-5)
<=> 3x2+334= 3x2-5x+18x-30
<=> 3x2-3x2+5x-18x=-30-334
<=>-13x=-364
<=>x=28
Vậy chiều rộng ban đầu là 28m
chiều dài ban đầu là 3.28=84(m)

a,
Xét Δ ABH và Δ CBA, có :
\(\widehat{ABH}=\widehat{CAB}\) (góc chung)
\(\widehat{AHB}=\widehat{CAB}=90^o\)
=> Δ ABH ~ Δ CBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> \(AB^2=BH.BC\)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (Py - ta - go)
=> \(BC^2=15^2+20^2\)
=> BC = 25 (cm)
Ta có : \(AB^2=BH.BC\) (cmt)
=> \(15^2=BH.25\)
=> BH = 9 (cm)
Ta có : BC = BH + CH
=> 25 = 9 + CH
=> CH = 16 (cm)
b,
Xét Δ AMN và Δ ACB, có :
\(\widehat{MAN}=\widehat{CAB}=90^o\)
\(\widehat{MAN}=\widehat{CAB}\) (góc chung)
=> Δ AMN ~ Δ ACB (g.g)
=> \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> AM.AB = AN.AC
Ta có : \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> \(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=> \(\dfrac{AN}{AM}=\dfrac{15}{20}=\dfrac{3}{4}\)
Vậy : ta có kết luận : Δ AMN = \(\dfrac{3}{4}\) Δ ACB
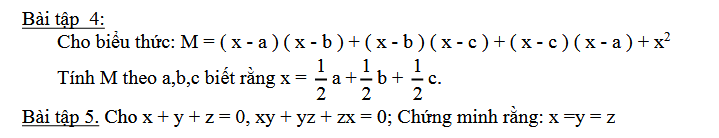

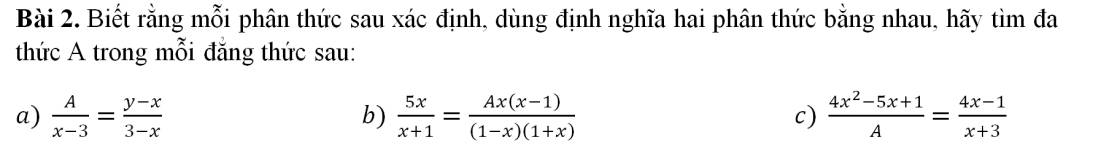 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ 





Bài 4:
$M=[x^2-(a+b)x+ab]+[x^2-(b+c)x+bc]+[x^2-(a+c)x+ac]+x^2$
$=4x^2-2(a+b+c)x+ab+bc+ac$
$=4x^2-2.2x.x+ab+bc+ac=4x^2-4x^2+ab+bc+ac$
$=ab+bc+ac$
Bài 5:
Ta có:
$(x+y+z)^2=0^2=0$
$\Leftrightarrow x^2+y^2+z^2+2(xy+yz+xz)=0$
$\Leftrightarrow x^2+y^2+z^2+0=0$
$\Leftrightarrow x^2+y^2+z^2=0$
Ta thấy: $x^2\geq 0; y^2\geq 0; z^2\geq 0$ với mọi $x,y,z\in\mathbb{R}$
Do đó để tổng của chúng bằng $0$ thì:
$x^2=y^2=z^2=0$
$\Leftrightarrow x=y=z=0$ (đpcm)