K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 4 2017
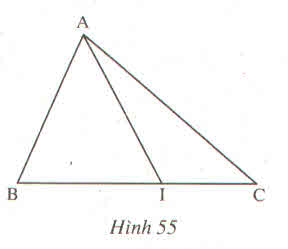
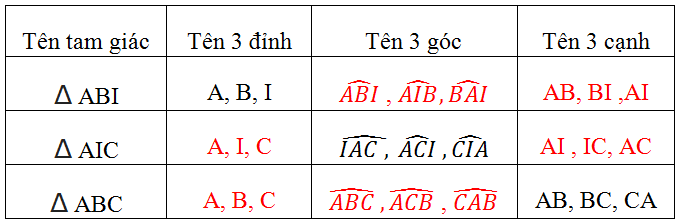
Giải:
|
Tên tam giác |
Tên 3 đỉnh |
Tên 3 góc |
Tên 3 cạnh |
|
|
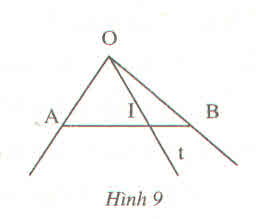
A,B,I |
|
AB, BI, IA |
|
|
A,I,C |
|
AI, IC, CA |
|
|
A,B,C |
|
AB, BC, CA |
SG
4
17 tháng 4 2017
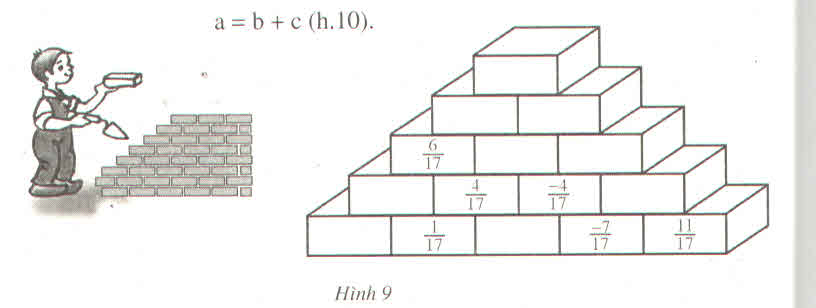
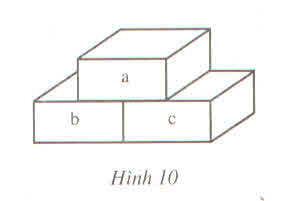
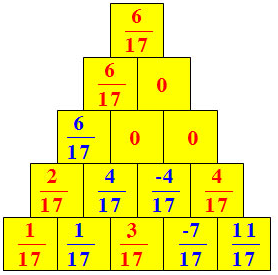
Làm theo quy tắc ở hình 10, ta có thể "xây tường" như sau:
18 tháng 4 2017
Giải:
|
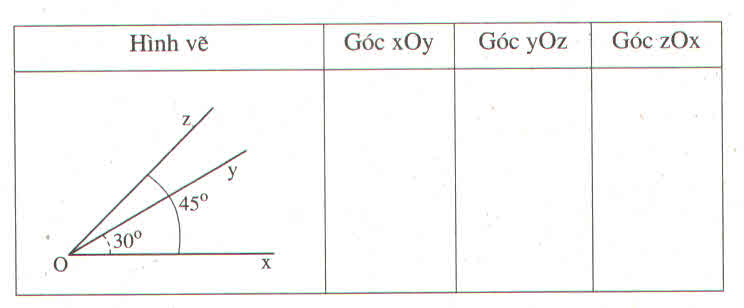
Hình |
Tên góc (cách viết thông thường) |
Tên đỉnh |
Tên cạnh |
Tên góc (Cách viết kí hiệu) |
|
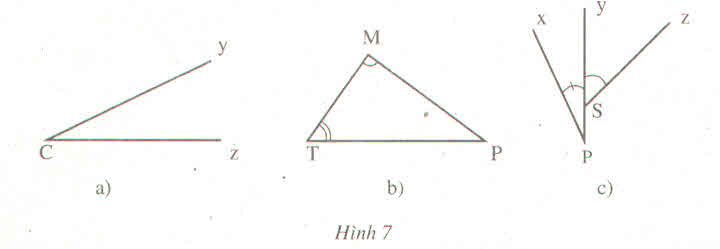
a |
Góc yCz, góc zCy, góc C |
C |
Cy,Cz |
|
|
b |
Góc MTP, PTM, T Góc TMP, PMT,M Góc TPM, MPT,P |
T M P |
TM,TP MT,MP PT,PM |
|
|
c |
Góc xPy,yPx,P Góc ySz,zSy |
P S |
Px, Py Sy, Sz |
|
SG
1
.9h sáng mai là em phải nộp bài rồi mà chưa biết giải
Em xin thề,ai giải giùm em(lời giải chi tiết
) em bái là sư phụ luôn
.Nhờ các bậc tiền bối chỉ bảo :
AT
5 tháng 7 2017
\(2\left(x-3\right)-3\left(1-2x\right)=4+4\left(1-x\right)\)
\(\Rightarrow2x-6-3+6x=4+4-4x\)
\(\Rightarrow2x+6x+4x=4+4+3+6\)
\(\Rightarrow12x=17\Rightarrow x=\dfrac{17}{12}\)
Vậy..................
5 tháng 7 2017
\(2\left(x-3\right)-3\left(1-2x\right)=4+4\left(1-x\right)\)
\(2x-6-3+6x=4+4-4x\)
\(8x-9=8-4x\)
\(8x=8-4x+9\)
\(8x=17-4x\)
\(12x=17\)
\(x=\dfrac{17}{12}\)
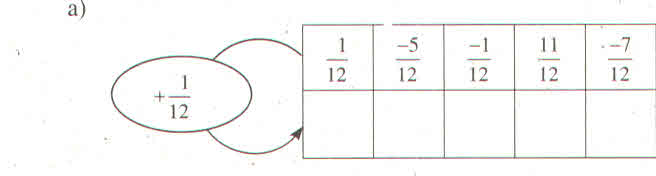
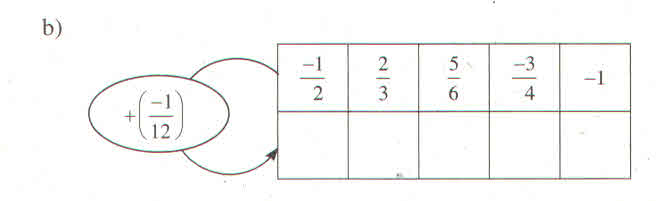
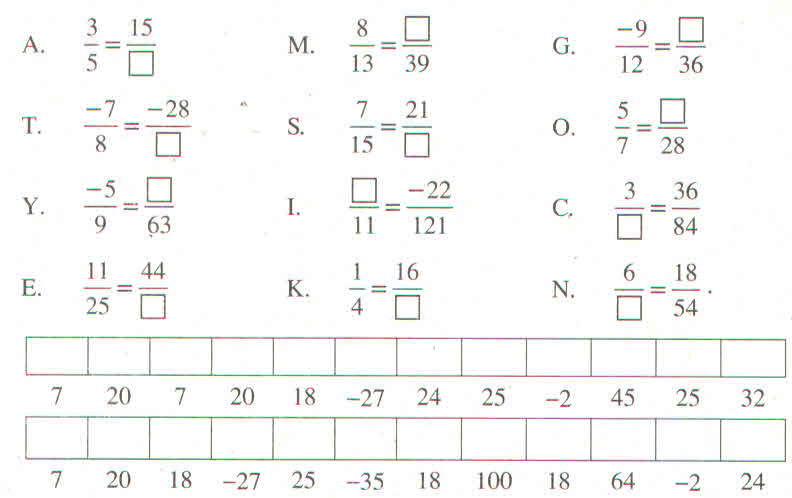
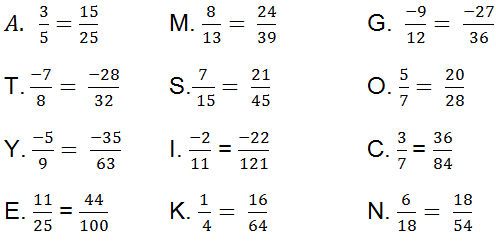
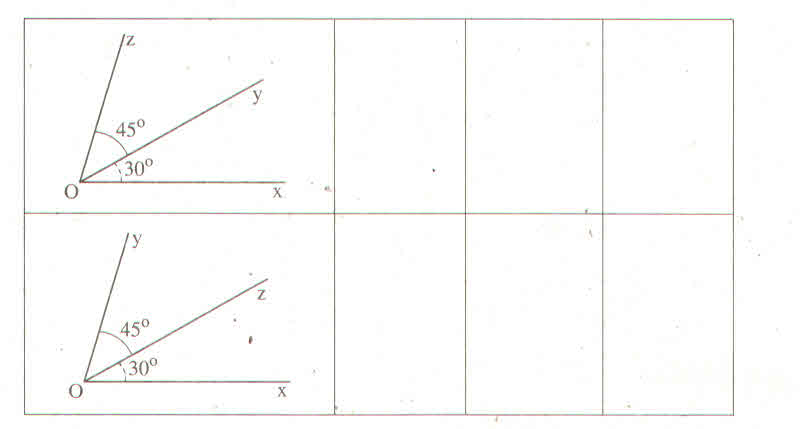
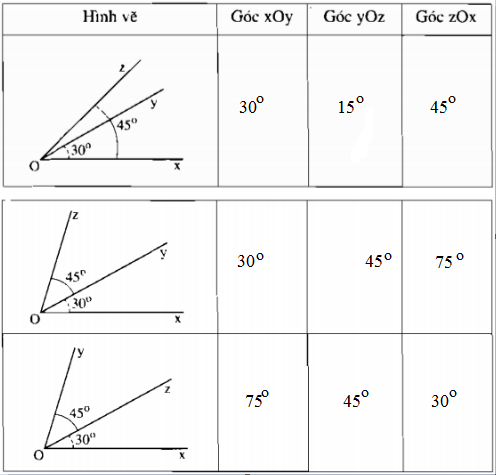
Bài 1 ý ạ
Tham khảo:v and nguồn: Tìm ba số tự nhiên khác nhau, biết tổng của chúng bằng tích của chúng.Đáp số: ba số đó là: câu hỏi 217719 - hoidap247.com
Giả sử a là số lớn nhất trong 3 số.
Ta có a + b + c = a.b.c < 3a ⇔ b.c <3.
Vì a, b, c là các số nguyên dương và b.c <3.
Do b, c nguyên dương nên tích b,c nguyên dương hay b.c = 1 hoặc b.c =2.
Mà a,b,c khác nhau nên b và c chỉ có thể là 1 và 2.
⇒ c =1 , b = 2. (vì b.c < 3)
Vậy ta có 1 + 2 + a = 1.2.a hay 3+a = 2a => a = 3
⇒Số cần tìm là 1, 2, 3