K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TK
2
21 tháng 11 2021
\(a^3b-ab^3=ab\left(a^2-b^2\right)=ab\left(a^2-ab+ab-b^2\right)=ab\left(a-b\right)\left(a+b\right)\)
Với a hoặc b chẵn \(\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮2\)
Với a và b lẻ \(\Leftrightarrow\left(a-b\right)⋮2\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮2\)
Vậy \(ab\left(a-b\right)\left(a+b\right)⋮2,\forall a,b\left(1\right)\)
Với a hoặc b chia hết cho 3 thì \(ab\left(a-b\right)\left(a+b\right)⋮3\)
Với \(a=3k+1;b=3q+1\Leftrightarrow\left(a-b\right)=3\left(k-q\right)⋮3\)
\(\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮3\)
Với \(a=3k+1;b=3q+2\Leftrightarrow\left(a+b\right)=\left(3k+1+3q+2\right)=3\left(k+q+1\right)⋮3\)
\(\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮3\)
Mà a,b có vai trò tương đương nên \(ab\left(a-b\right)\left(a+b\right)⋮3,\forall a,b\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrowđpcm\)
21 tháng 11 2021
Ta có : a3b -ab3
=a3b -ab -ab3 +ab
=ab (a2 -1) -ab (b2 -1)
=ab (a-1)(a+1) -ab (b-1)(b+1)
Vì a (a-1)(a+1) là 3 số tự nhiên liên tiếp nên chia hết cho 6 .Tương tự b (b-1)(b+1) cũng chia hết cho 6
=> a3b -ab3 chia hết cho 6 (đpcm )
DB
4
9 tháng 7 2019
65 - 5 . ( x + 2 ) = 15
5 . ( x + 2 ) = 65 - 15
5 . ( x + 2 ) = 50
( x + 2 ) = 50 : 5
x + 2 = 10
x = 8
Vậy x = 8
9 tháng 7 2019
\(65-5.\left(x+2\right)=15\)
\(5\left(x+2\right)=50\)
\(x+2=10\)
\(x=8\)
TP
5
18 tháng 5 2020
Bài làm
Bạn hamlon bên dưới không làm được vậy để mình làm cho bạn .
\(\frac{3}{5}.\frac{3}{7}+\frac{3}{5}.\frac{2}{9}-\frac{3}{5}.\frac{3}{11}\)
\(=\frac{3}{5}\left(\frac{3}{7}+\frac{2}{9}-\frac{3}{11}\right)\)
\(=\frac{3}{5}.\left(\frac{297}{693}+\frac{154}{693}-\frac{189}{693}\right)\)
\(=\frac{3}{5}.\frac{262}{693}\)
\(=\frac{262}{1155}\)
18 tháng 6 2023
3:
a: =8/24+9/24-14/24=3/24=1/8
b: =-12/56+35/56-28/56=-5/56
c: =9/36-24/36-22/36=-37/36
d: \(=\dfrac{6}{24}+\dfrac{10}{24}-\dfrac{21}{24}-\dfrac{1}{13}=\dfrac{-5}{24}-\dfrac{1}{13}=\dfrac{-89}{24\cdot13}\)
TT
0
HL
2
AH
Akai Haruma
Giáo viên
26 tháng 11 2023
1/
$C=5+(5^2+5^3)+(5^4+5^5)+.....+(5^{2022}+5^{2023})$
$=5+5^2(1+5)+5^4(1+5)+....+5^{2022}(1+5)$
$=5+(1+5)(5^2+5^4+....+5^{2022})$
$=5+6(5^2+5^4+....+5^{2022})$
$\Rightarrow C$ chia $6$ dư $5$
$\Rightarrow C\not\vdots 6$
AH
Akai Haruma
Giáo viên
26 tháng 11 2023
2/
$D=(1+2+2^2)+(2^3+2^4+2^5)+....+(2^{2019}+2^{2020}+2^{2021})$
$=(1+2+2^2)+2^3(1+2+2^2)+....+2^{2019}(1+2+2^2)$
$=(1+2+2^2)(1+2^3+...+2^{2019})$
$=7(1+2^3+...+2^{2019})\vdots 7$
Ta có đpcm.
IK
3
22 tháng 1 2022
Đặt A = 13 + 23 + 32 +...+ 20213
A = 1 + (1.2.3+2) + (2.3.4+3) +...+(2020.2021.2022+2021)
A = ( 1+2+3+...+2021) + ( 1.2.3+2.3.4+...+2020.2021.2022)
Đặt B = 1+2+3+...+2021
B = 2022.2021:2= 2043231
Đặt C = 1.2.3+2.3.4+...+2020.2021.2022
4C = 4.(1.2.3+2.3.4+...+2020.2021.2022)
4C = 1.2.3.4+2.3.4.4+...+2020.2021.2022.4
4C = 1.2.3.4+2.3.4.(5-1)+...+2020.2021.2022.(2023-2019)
4C = 1.2.3.4+2.3.4.5-1.2.3.4+...+2020.2021.2022.2023-2019.2020.2021.2022
4C = (1.2.3.4+2.3.4.5+...+2020.2021.2022.2023) - ( 1.2.3.4+2.3.4.5+2019.2020.2021.2022)
4C = 2020 . 2021 . 2022 . 2023
C = \(\frac{2020.2021.2022.2023}{4}\)
=> A = 2043231 + \(\frac{2020.2021.2022.2023}{4}\)
Vậy giá trị của biểu thức 13 + 23 +...+ 20213 = 2043231 +\(\frac{2020.2021.2022.2023}{4}\)
_HT_
3 tháng 3 2022
B = 1 + 3 + 3 2 + . . . + 3 2021 = > 3 B = 3 + 3 2 + 3 3 + . . . + 3 2022 = > 3 B − B = 3 2022 − 1 = > 2 B = 3 2022 − 1 = > B = 3 2022 − 1 2 V ậ y B = 3 2022 − 1 2
HT
@SKY LẠNH LÙNG
TT
2
LT
16 tháng 9 2019
847 + 2 x 81 +53=847+162+53 = 847 + 53+47 +62 +53 = ( 847 + 53 ) + ( 47+53 ) + 62 = 900 + 100 + 62 = 1000 + 62 = 1062 hok tot
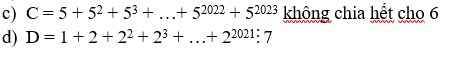
\(\Rightarrow5\left(x+2\right)+4⋮x+2\\ \Rightarrow x+2\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Rightarrow x\in\left\{-6;-4;-3;-1;0;2\right\}\)
⇒5(x+2)+4⋮x+2
⇒x+2∈Ư(4)={−4;−2;−1;1;2;4}
⇒x∈{−6;−4;−3;−1;0;2}