
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=\(\left(\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}}{\sqrt{x}+3}\right).\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
=\(\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)+\sqrt{x}\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(x-9\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
=\(\dfrac{2x+6\sqrt{x}+\sqrt{x}\left(x-\sqrt{x}-6\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}.\dfrac{1}{\sqrt{x}}\)
=\(\dfrac{2x+6\sqrt{x}+x\sqrt{x}-x-6\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+x\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)
=\(\dfrac{x+\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}+2\right)}\)

Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)

\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}+\dfrac{1}{2-\sqrt{x}}\left(đk:x\ge0;x\ne4\right)\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-2}\)
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{3+2\sqrt{x}-4-\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(X=\dfrac{1}{\sqrt{x}+1}\)
\(S=\left(\dfrac{1}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\left(đk:x\ge0;x\ne1\right)\)
\(S=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\)
\(S=\dfrac{\sqrt{x}-2+x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{x+4\sqrt{x}+4}{1-\sqrt{x}}\)
\(S=\dfrac{x+3\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)
\(S=\dfrac{\left(x+3\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\left(1-\sqrt{x}\right)}\)
(đến đoạn này thì trong ngoặc ko tách ra đc nữa nên mik nghĩ là đến đây là xong, nếu sai thì bn nói mik)

\(H=\dfrac{x+5\sqrt{x}+6+x-3\sqrt{x}+2-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}:\dfrac{\sqrt{x}-2+5}{\sqrt{x}-2}\)
\(=\dfrac{2x-2\sqrt{x}+12}{\sqrt{x}+2}\cdot\dfrac{1}{\sqrt{x}+3}\)
\(I=\dfrac{3x+3-2x+6\sqrt{x}-x-3\sqrt{x}}{x-9}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)
\(=\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{3}{\sqrt{x}+3}\)

\(M=\left(\dfrac{\sqrt{x}}{2x}-\dfrac{1}{\sqrt{x}}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\right)\\ =\left(\dfrac{\sqrt{x}}{2x}-\dfrac{2\sqrt{x}}{2x}\right)\cdot\left(\dfrac{\left(\sqrt{x}-1\right)^2-\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\\ =\dfrac{x-2\sqrt{x}}{2x}\cdot\dfrac{x-2\sqrt{x}+1-\left(x+2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{x-2\sqrt{x}+1-x-2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2x}\cdot\dfrac{-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-2\right)}{x-1}\)

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)

\(15,A=\dfrac{x-1-4\sqrt{x}+4+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ A=\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\\ 16,B=\dfrac{\sqrt{x}\left(x\sqrt{x}-1\right)}{x+\sqrt{x}+1}-\dfrac{2\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}+\dfrac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-2\left(\sqrt{x}+1\right)+2\left(\sqrt{x}+1\right)\\ B=x-\sqrt{x}-2\sqrt{x}-2+2\sqrt{x}+2=x-\sqrt{x}\)

15. \(=\dfrac{x-1-4\left(\sqrt{x}-1\right)+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{x-4\sqrt{x}+4}{x-1}.\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\left(\sqrt{x}-2\right)^2.\dfrac{1}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\)

\(C=\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}-1}-\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{\left(\sqrt{a}+1\right)^2}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}+1}{\sqrt{a}+1}=\dfrac{a+2\sqrt{a}+1-a-\sqrt{a}-1}{\sqrt{a}+1}\)
\(=\dfrac{\sqrt{a}}{\sqrt{a}+1}\)

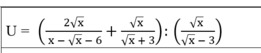

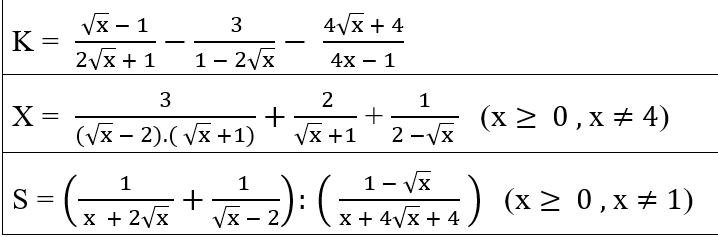
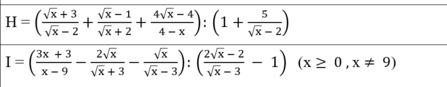
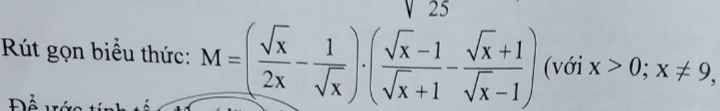
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.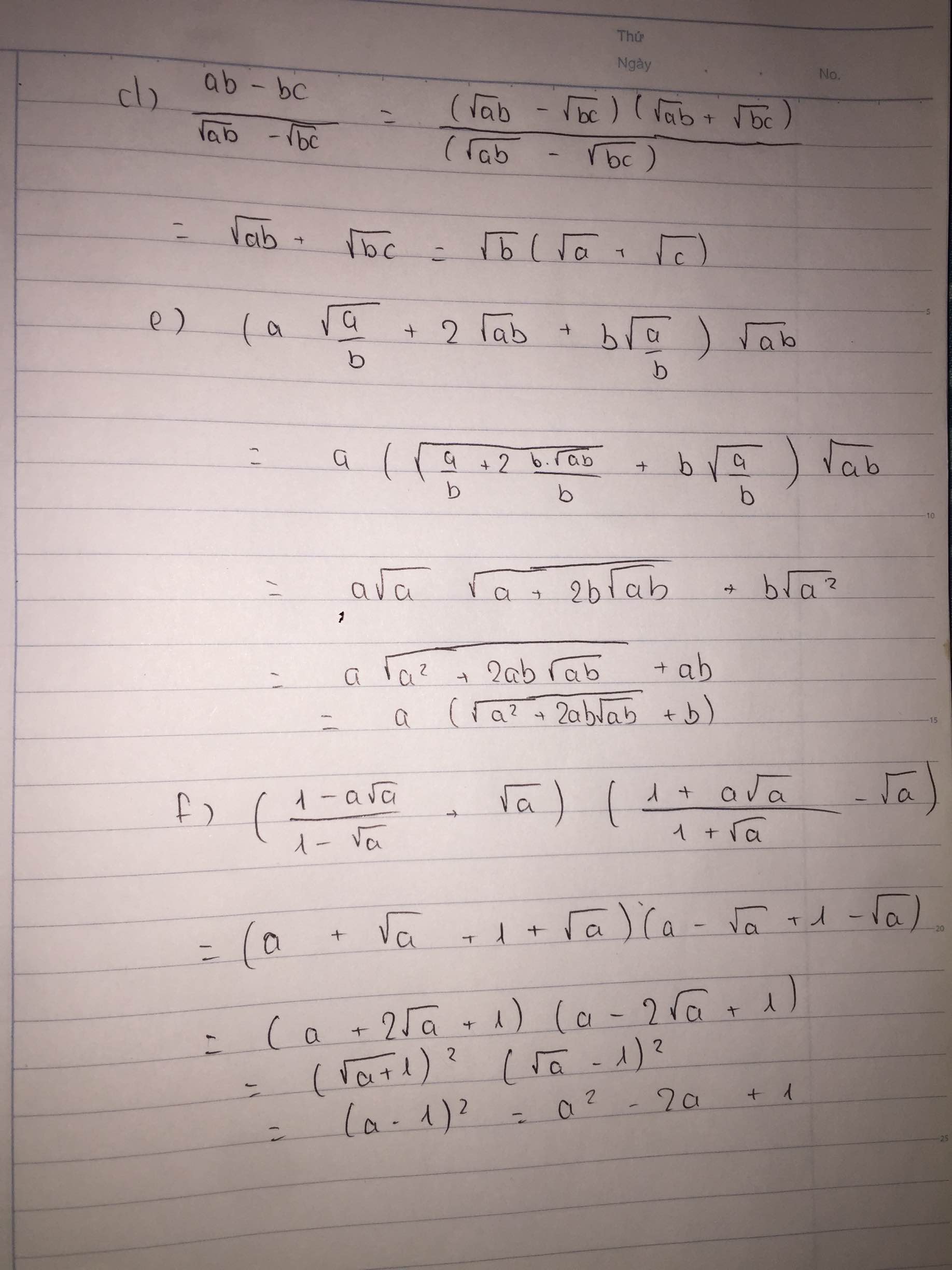
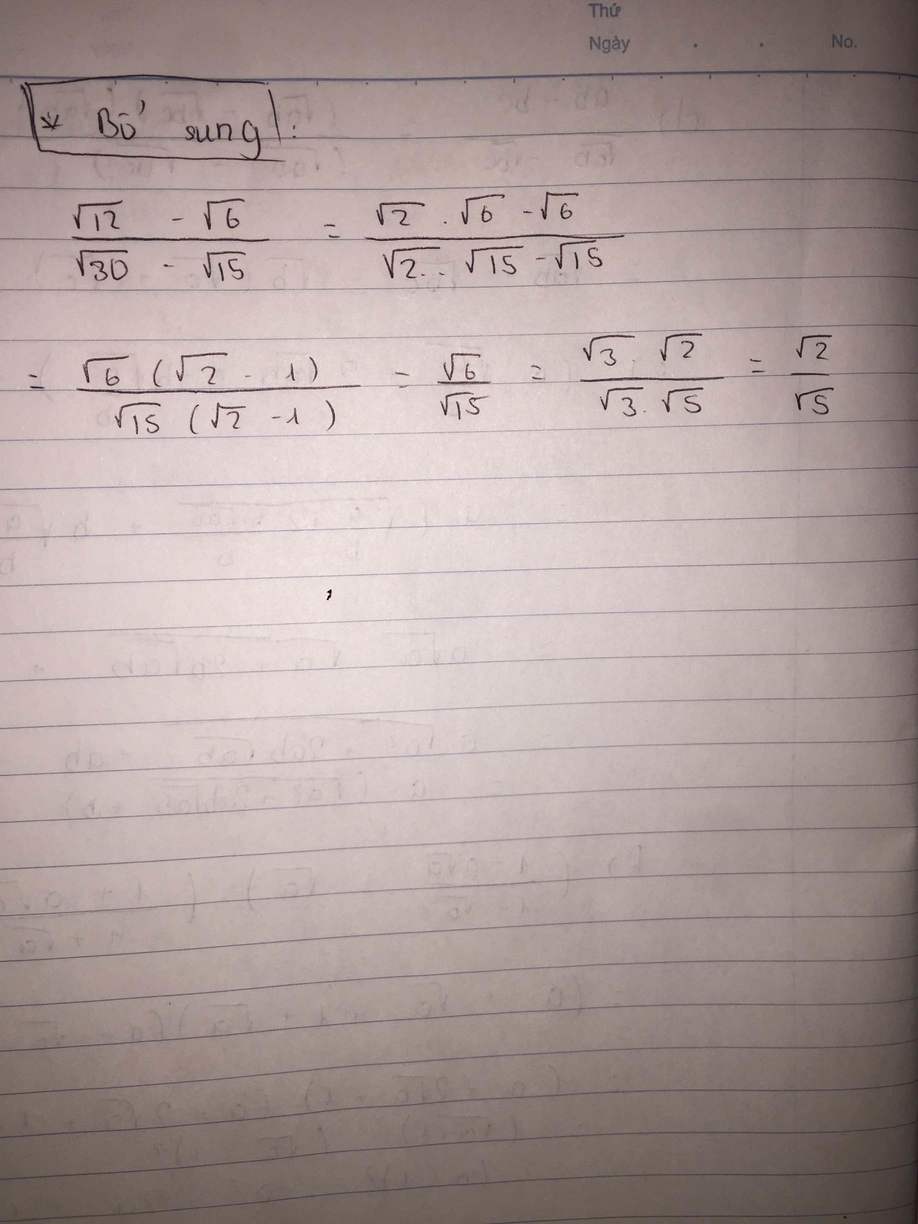



\(\sqrt{0,81.a^{10}\left(x^2-2x+1\right)}=\sqrt{\left(0,9\right)^2.\left(a^5\right)^2\left(x-1\right)^2}\)
\(=0,9.\left|a^5\left(x-1\right)\right|=0,9.\left|a^5x-a^5\right|\)