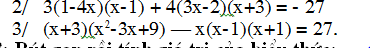Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(3\left(x-2\right)^2+\left(x-1\right)^3-x^3=-7\)
\(\Leftrightarrow3x^2-12x+12+x^3-3x^2+3x-1-x^3=-7\)
\(\Leftrightarrow-9x=-18\)
hay x=2
b: ta có: \(\left(x+2\right)^3-x\left(x-1\right)\left(x+1\right)=6x^2-5x+3\)
\(\Leftrightarrow x^3+6x^2+12x+8-x^3+x-6x^2+5x-3=0\)
\(\Leftrightarrow17x=-5\)
hay \(x=-\dfrac{5}{17}\)
c: Ta có: \(\left(2x-1\right)^3+12\left(x-1\right)\left(x+1\right)=14x-13\)
\(\Leftrightarrow8x^3-12x^2+6x-1+12x^2-12-14x+13=0\)
\(\Leftrightarrow8x^3-8x=0\)
\(\Leftrightarrow8x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
a) \(3\left(x-2\right)^2+\left(x-1\right)^3-x^3=-7\)
\(\Rightarrow3x^2-12x+12+x^3-3x^2+3x-1-x^3=-7\)
\(\Rightarrow-9x=-18\)
\(\Rightarrow x=2\)
b) \(\left(x+2\right)^3-x\left(x-1\right)\left(x+1\right)=6x^2-5x+3\)
\(\Rightarrow x^3+6x^2+12x+8-x^3+x=6x^2-5x+3\)
\(\Rightarrow18x=-5\)
\(\Rightarrow x=-\dfrac{5}{18}\)
c) \(\left(2x-1\right)^3+12\left(x-1\right)\left(x+1\right)=14x-13\)
\(\Rightarrow8x^3-12x^2+6x-1+12x^2-12=14x-13\)
\(\Rightarrow8x^3-8x=0\)
\(\Rightarrow8x\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)


Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\)(1)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\)(2)
Ta có: M là trung điểm của BC(gt)
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay DE//BC(đpcm)


\(A=\dfrac{1}{16}c^2-9c+10=\dfrac{1}{16}\left(x-72\right)^2-314\ge-314\)
\(A_{min}=-314\) khi \(c=72\)
\(B=\left(d^2-6de+9e^2\right)+\left(e^2-10e+25\right)+1=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\)
\(B_{min}=1\) khi \(\left\{{}\begin{matrix}d=15\\e=5\end{matrix}\right.\)
\(C=4x^4+12x^2+11\)
Do \(\left\{{}\begin{matrix}x^4\ge0\\x^2\ge0\end{matrix}\right.\) ; \(\forall x\Rightarrow C\ge11\)
\(C_{min}=11\) khi \(x=0\)
a) Ta có: \(\dfrac{1}{16}c^2-9c+10\)
\(=\left(\dfrac{1}{4}c\right)^2-2\cdot\dfrac{1}{4}c\cdot18+324-314\)
\(=\left(\dfrac{1}{4}c-18\right)^2-314\ge-314\forall c\)
Dấu '=' xảy ra khi \(\dfrac{1}{4}c=18\)
hay c=72
Vậy: Giá trị nhỏ nhất của biểu thức \(\dfrac{1}{16}c^2-9c+10\) là -314 khi c=72
b) Ta có: \(d^2+10e^2-6de-10e+26\)
\(=d^2-6de+9e^2+e^2-10e+25+1\)
\(=\left(d-3e\right)^2+\left(e-5\right)^2+1\ge1\forall d,e\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}e=5\\d=3e=3\cdot5=15\end{matrix}\right.\)
Vậy: Giá trị nhỏ nhất của biểu thức \(d^2+10e^2-6de-10e+26\) là 1 khi e=5 và d=15
c) Ta có: \(4x^4+12x^2+11\)
\(=4x^4+12x^2+9+2\)
\(=\left(2x^2+3\right)^2+2\ge3^2+2=11\)
Dấu '=' xảy ra khi x=0
Vậy: Giá trị nhỏ nhất của biểu thức \(4x^4+12x^2+11\) là 11 khi x=0

3: Ta có: \(\left(x+3\right)\left(x^2-3x+9\right)-x\left(x-1\right)\left(x+1\right)=27\)
\(\Leftrightarrow x^3-27-x^3+x=27\)
hay x=54

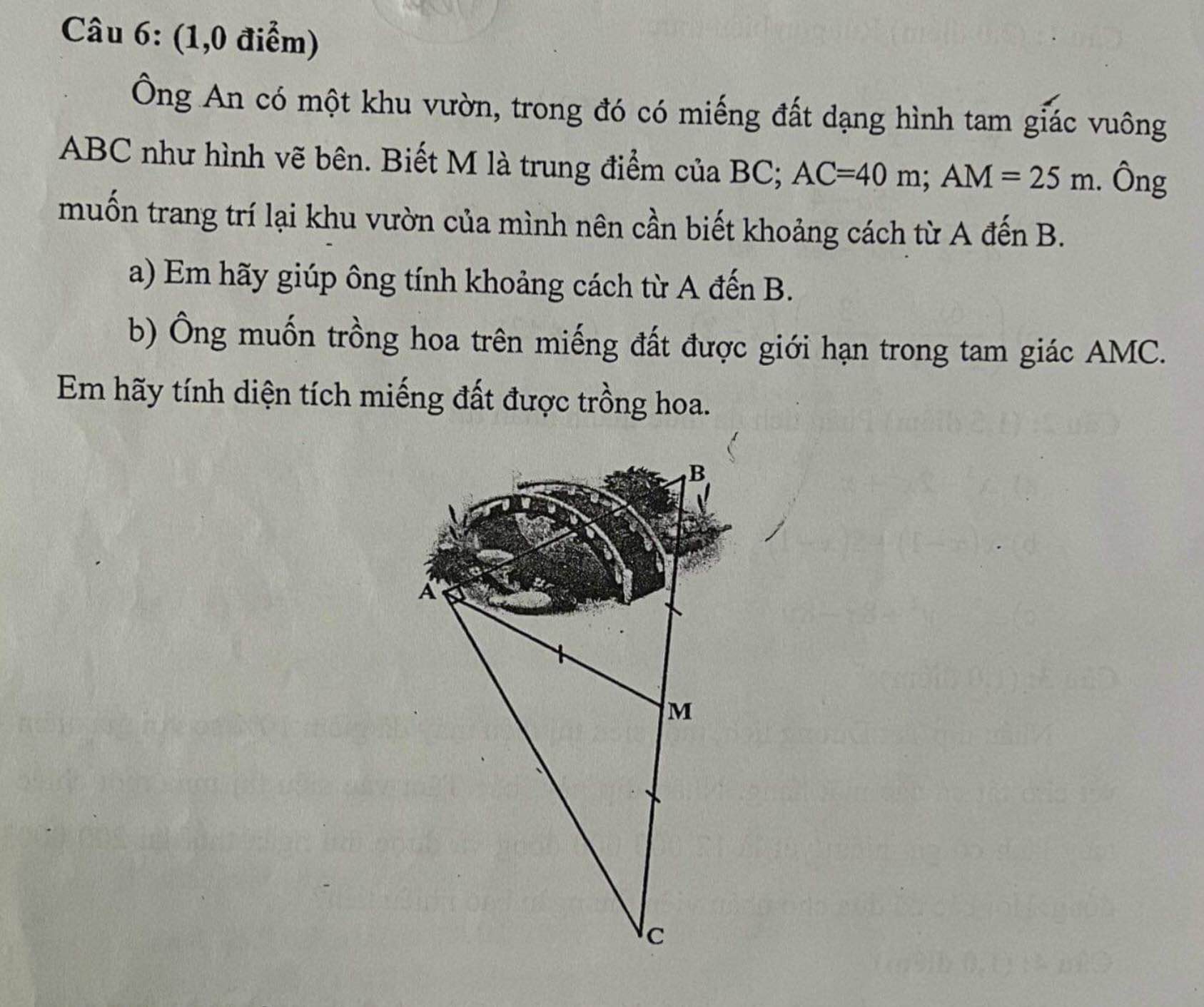
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)

Tìm ba số tự nhiên liên tiếp biết rằng cộng ba tích mỗi tích là tích của hai trong ba số đó thì đc 26
Tớ cũng hỏi thầy r nhưng th bảo là k sai đề đou =((( chính xác là 5 tích ạ =(((
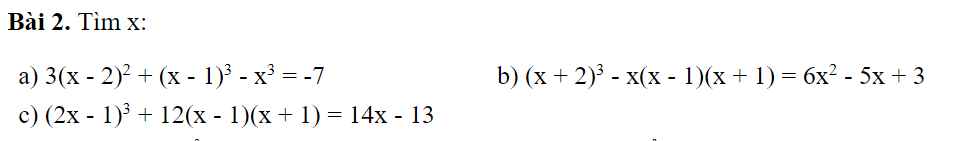 giúp với em sắp phải nộp deadline r ạ:((
giúp với em sắp phải nộp deadline r ạ:((