
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(f'\left(x\right)=-sinx\Rightarrow f'\left(\dfrac{\pi}{4}\right)=-sin\left(\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
\(g'\left(x\right)=-\dfrac{1}{cos^2x}\Rightarrow g'\left(\dfrac{\pi}{4}\right)=-\dfrac{1}{cos^2\left(\dfrac{\pi}{4}\right)}=-2\)
\(\Rightarrow\dfrac{f'\left(\dfrac{\pi}{4}\right)}{g'\left(\dfrac{\pi}{4}\right)}=\dfrac{\sqrt{2}}{4}\)

3.
\(cosx=t\in\left[-1;1\right]\Rightarrow y=f\left(t\right)=-t^2-2t+1\)
\(-\dfrac{b}{2a}=-1\)
\(f\left(-1\right)=2\) ; \(f\left(1\right)=-2\)
\(\Rightarrow-2\le y\le2\Rightarrow\) có 5 giá trị nguyên của T
4.
\(cos^2x-cosx-2=0\Rightarrow\left[{}\begin{matrix}cosx=-1\\cosx=2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x=\pi+k2\pi\)
\(\Rightarrow x=\left\{\pi;3\pi\right\}\Rightarrow\pi.3\pi=3\pi^2\)

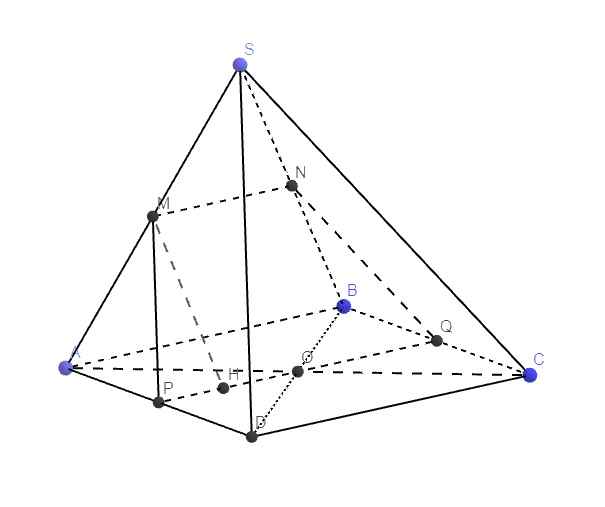
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)

4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)

4.
b, \(2sin^2\dfrac{x}{2}-5sin\dfrac{x}{2}+3=0\)
\(\Leftrightarrow\left(sin\dfrac{x}{2}-1\right)\left(2sin\dfrac{x}{2}-3\right)=0\)
\(\Leftrightarrow sin\dfrac{x}{2}=1\)
\(\Leftrightarrow\dfrac{x}{2}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\pi+k2\pi\)
3.
a, \(3cos^2\dfrac{x}{2}-4cos\dfrac{x}{2}+1=0\)
\(\Leftrightarrow\left(cos\dfrac{x}{2}-1\right)\left(3cos\dfrac{x}{2}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\dfrac{x}{2}=1\\cos\dfrac{x}{2}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pi+k2\pi\\x=\pm2arccos\dfrac{1}{3}+k2\pi\end{matrix}\right.\)

Bạn cần giúp câu nào nhỉ?
Nếu cần hết thì nên chia nhỏ từng câu ra, nhiều quá người khác nhìn sẽ bị ngộp, không ai muốn làm đâu






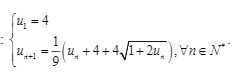 giúp em với mọi người ơi:(
giúp em với mọi người ơi:(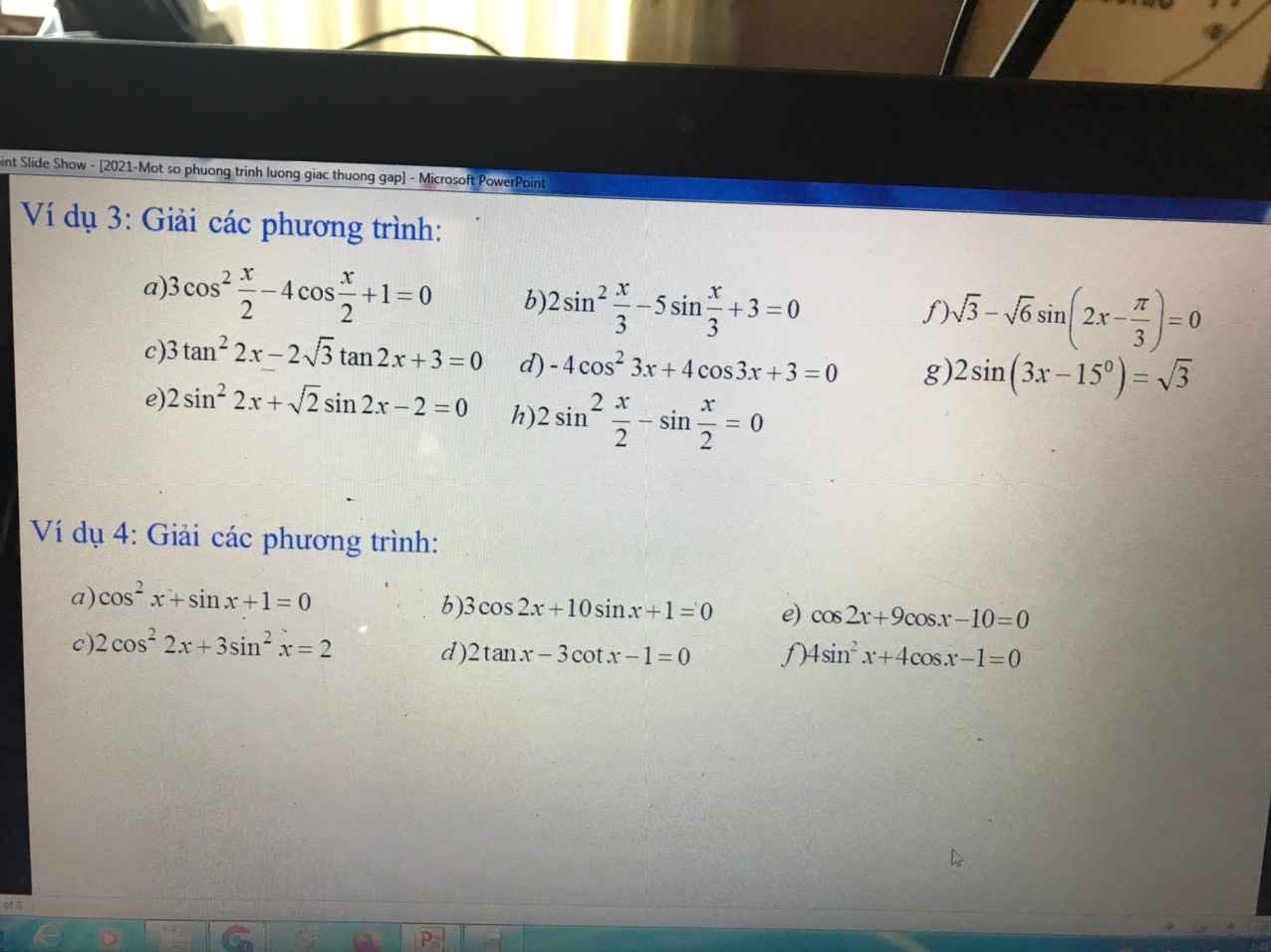



Không gian mẫu: \(6^2=36\)
Các biến cố thuận lợi: (1;6);(6;1);(2;5);(5;2);(3;4);(4;3) có 6 biến cố
Xxacs suất: \(\dfrac{6}{36}=\dfrac{1}{6}\)