
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Rút gọn được \(A=\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(B-8A\le0\Leftrightarrow\dfrac{x+16}{\sqrt{x}-3}-\dfrac{8\sqrt{x}}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{x-8\sqrt{x}+16}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-4\right)^2}{\sqrt{x}-3}\le0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-4=0\\\sqrt{x}-3< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=16\\x< 9\end{matrix}\right.\)
Kết hợp ĐKXD ta được: \(\left[{}\begin{matrix}x=16\\0\le x< 9\end{matrix}\right.\)



a) \(\left\{{}\begin{matrix}x\ge0\\x\ne\dfrac{5}{3}\end{matrix}\right.\)
b) \(x\ne\dfrac{1}{2}\)
c) \(\left[{}\begin{matrix}x>\dfrac{1}{2}\\x< -5\end{matrix}\right.\)

c. Dễ chứng minh 5 điểm A, N, F, H, E cùng thuộc đường tròn đường kính AH.
\(\Rightarrow HN\perp AN\left(1\right)\)
Vẽ đường kính AM của (O) \(\Rightarrow MN\perp AN\left(2\right)\)
Từ (1), (2) suy ra 3 điểm M, H, N thẳng hàng (3)
Dễ chứng minh BHCM là hình bình hành (BH // CM do cùng vuông góc với AC, tương tự 2 cạnh còn lại)
\(\Rightarrow\) 3 điểm H, I, M thẳng hàng (4)
Từ (3), (4) suy ra 3 điểm N, H, I thẳng hàng.


b: =(m-1)^2-4(-m^2-2)
=m^2+2m+1+4m^2+8
=5m^2+2m+9
=5(m^2+2/5m+9/5)
=5(m^2+2*m*1/5+1/25+44/25)
=5(m+1/5)^2+44/5>=44/5>0 với mọi m
=>PT luôn có hai nghiệm pb


Bài 2a
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=BH.CH\Rightarrow CH=\frac{AH^2}{BH}=\frac{256}{25}\)cm
-> BC = HB + CH = \(25+\frac{256}{25}=\frac{881}{25}\)cm
Áp dụng định lí Pytago của tam giác ABH vuông tại H
\(AB=\sqrt{AH^2+HB^2}=\sqrt{881}\)cm
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=18,9...\)cm
Bài 2c
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức :
\(AH^2=HB.HC=3.4=12\Rightarrow AH=2\sqrt{3}\)cm
Theo định lí Pytago tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+HB^2}=\sqrt{21}\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{12}=\frac{1}{21}+\frac{1}{AC^2}\Rightarrow AC=2\sqrt{7}\)cm

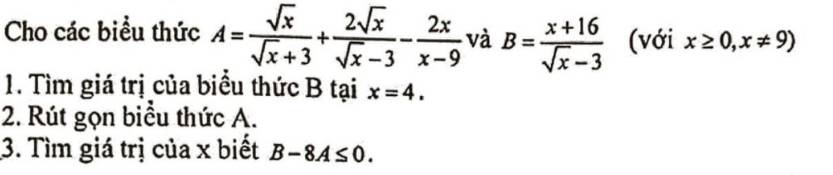








c: góc MCK=góc MAC
góc NAE=góc MCI
=>góc MCK=góc MCI
Chứng minh tương tự, ta được: góc MBK=góc MBI
=>I đối xứng K qua BC
vì sao góc MAC = góc NAE vậy ạ