
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔOCB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc CB
Vì góc OIA=góc OMA=góc ONA
nên O,M,N,I,A cùng thuộc 1 đường tròn
b: Xét ΔABN và ΔANC có
góc ABN=góc ANC
góc BAN chung
=>ΔABN đồng dạng với ΔANC
=>AB/AN=AN/AC
=>AN^2=AB*(AB+BC)
=>4*(BC+4)=6^2=36
=>BC=5cm

\(a,\Leftrightarrow5x-3=4\Leftrightarrow x=\dfrac{12}{5}\\ b,ĐK:x\ge0\\ PT\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}+6=4\sqrt{x}+30\\ \Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ c,ĐK:x\ge-2\\ PT\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-15=2\sqrt{x+2}+12\\ \Leftrightarrow9\sqrt{x+2}=27\\ \Leftrightarrow\sqrt{x+2}=3\\ \Leftrightarrow x+2=9\\ \Leftrightarrow x=7\left(tm\right)\\ d,\Leftrightarrow\left|x\right|=13\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-13\end{matrix}\right.\)
a: \(\Leftrightarrow5x-3=4\)
hay \(x=\dfrac{7}{5}\)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

Gọi giao điểm AE và BP là F;
Gọi giao điểm QD và AB là H;
Gọi kéo dài AD cắt BF tại P'
Dễ cm M là trung điểm AC
Xét \(\Delta OMC\) có QD//CM\(\Rightarrow\dfrac{OD}{OM}=\dfrac{QD}{CM}\)(hệ quả tales)
Tương tự với \(\Delta OAM\) có \(\dfrac{OD}{OM}=\dfrac{DH}{AM}\)
\(\Rightarrow\dfrac{QD}{CM}=\dfrac{DH}{AM}\)
Mà CM=AM (vì M là tđ AC)
\(\Rightarrow QD=DH\)
Dễ cm P là trung điểm BF
Xét \(\Delta ABP'\) có DH//BP'
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{AD}{AP'}\)(tales)
Tương tự với \(\Delta AFP'\) có \(\dfrac{QD}{FP'}=\dfrac{AD}{AP'}\)
\(\Rightarrow\dfrac{DH}{BP'}=\dfrac{QD}{FP'}\)
Mà DH=QD (cmt)
\(\Rightarrow BP'=FP'\)
\(\Rightarrow\)P' là trung điểm BF
\(\Rightarrow P\equiv P'\)
\(\Rightarrow A,D,P\) thẳng hàng


$A=x-3\sqrt{x}+1=(x-3\sqrt{x}+\frac{9}{4})-\frac{5}{4}$
$=(\sqrt{x}-\frac{3}{2})^2-\frac{5}{4}$
$\geq \frac{-5}{4}$
Vậy $A_{\min}=-\frac{5}{4}$. Giá trị này đạt tại $\sqrt{x}-\frac{3}{2}=0\Leftrightarrow x=\frac{9}{4}$
----------------
$B=\frac{3\sqrt{x}-1}{\sqrt{x}+2}=3-\frac{5}{\sqrt{x}+2}$
Vì $\sqrt{x}\geq 0$ nên $\sqrt{x}+2\geq 2$
$\Rightarrow \frac{5}{\sqrt{x}+2}\leq \frac{5}{2}$
$\Rightarrow B\geq 3-\frac{5}{2}=\frac{1}{2}$
Vậy $B_{\min}=\frac{1}{2}$ khi $x=0$
$C=\frac{\sqrt{x}(\sqrt{x}+3)-3(\sqrt{x}+3)+19}{\sqrt{x}+3}$
$=\sqrt{x}-3+\frac{19}{\sqrt{x}+3}$
$=(\sqrt{x}+3)+\frac{19}{\sqrt{x}+3}-6$
$\geq 2\sqrt{19}-6$ theo BĐT Cô-si
Dấu "=" xảy ra khi $(\sqrt{x}+3)^2=19\Leftrightarrow x=28-6\sqrt{19}$

1/ Tại x = 4, ta có: \(A=\dfrac{3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{4}+3}=\dfrac{3}{2+3}=\dfrac{3}{5}\)
➤ Với \(x=4\) thì \(A=\dfrac{3}{5}\)

b: \(\Leftrightarrow x\sqrt{2}=2\sqrt{2}+5\sqrt{2}=7\sqrt{2}\)
hay x=7


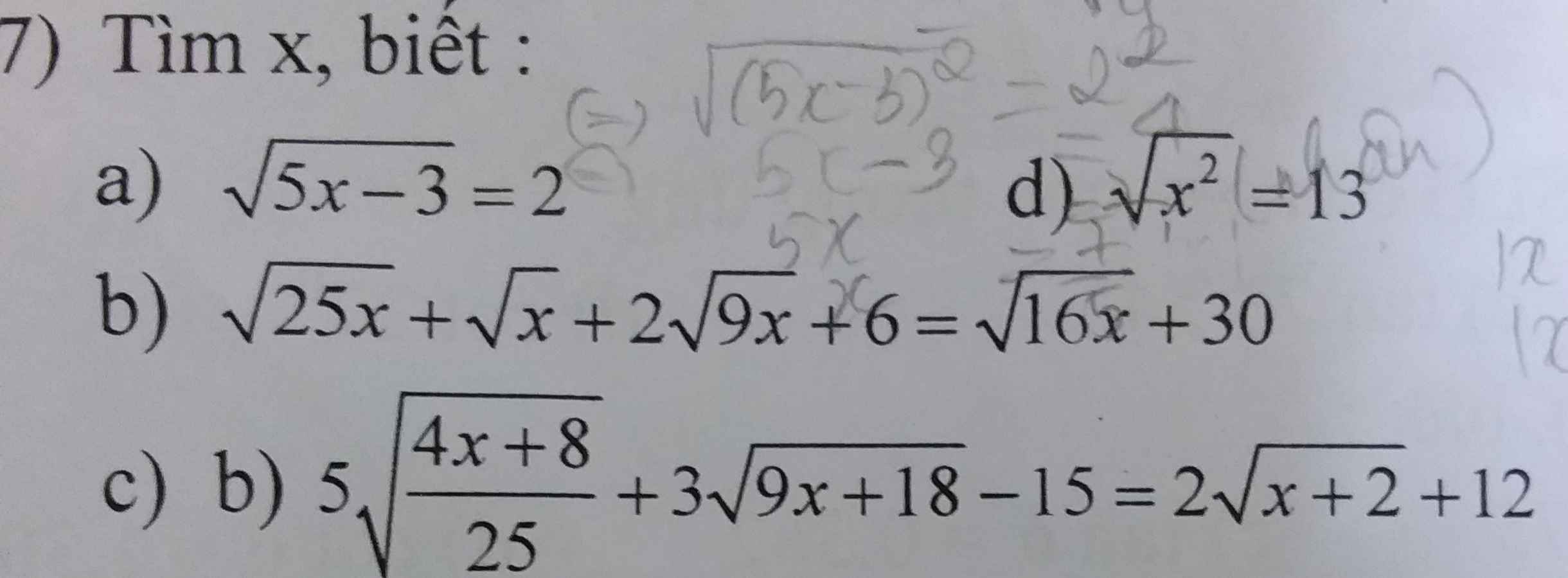
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp


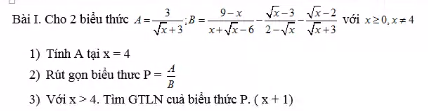

1: Thay x=25 vào A, ta được:
\(A=\dfrac{5-3}{2\cdot5+6}=\dfrac{2}{16}=\dfrac{1}{8}\)
2: \(B=\dfrac{x+16-5\sqrt{x}-10}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\)