K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
16 tháng 8 2023
11:
a: ABCD là hình chữ nhật
=>vecto AB+vecto AD=vecto AC
\(AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)
\(\left|\overrightarrow{AB}+\overrightarrow{AD}\right|=\left|\overrightarrow{AC}\right|=AC=5a\)
b: Gọi M là trung điểm của BC
=>BM=MC=4a/2=2a
Trên tia đối của tia MA lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}=2\cdot\overrightarrow{AM}\)
\(AM=\sqrt{AB^2+BM^2}=\sqrt{\left(3a\right)^2+\left(2a\right)^2}=a\sqrt{13}\)
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)
15 tháng 8 2023
11:
a: \(BD=AC=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)
|vecto AB+vecto AD|
=|vecto AB+vecto BC|
=|vecto AC|
=5a
b: Gọi M là trung điểm của BC
=>BM=CM=BC/2=2a
\(AM=\sqrt{AB^2+BM^2}=a\sqrt{13}\)
Xét ΔABC có AM là trung tuyến
nên vecto AB+vecto AC=2*vecto AM
=>|vecto AB+vecto AC|=2|vecto AM|
=>\(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=2\cdot AM=2a\sqrt{13}\)
26 tháng 11 2021
Câu 12:
b) mx2+2(m+3)x+m=0
(a = m; b = 2(m+3); c = m)
PT có 2 nghiệm cùng dấu ⇔ \([_{P>0}^{\Delta\ge0}\)
⇔ \([_{\dfrac{c}{a}}^{b^2-4ac}\)⇔\([_{\dfrac{m}{m}>0}^{[2\left(m+3\right)]^2-4.m.m\ge0}\)⇔\([_{1>0\left(LĐ\right)}^{4\left(m+3\right)^2-4m^2\ge0}\)⇔\(4\left(m^2+6m+9\right)-4m^2\ge0\)
⇔4m2+24m+36-4m2≥0 ⇔ 24m+36≥0⇔ m ≥ \(-\dfrac{3}{2}\)
Vậy với m ≥\(-\dfrac{3}{2}\)thì PT có 2 nghiệm cùng dấu.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 3 2022
11.
Đường tròn (C) tâm \(I\left(4;3\right)\) bán kính \(R=\sqrt{2}\)
\(d\left(I;\Delta\right)=\dfrac{\left|4+3-11\right|}{\sqrt{1^2+1^2}}=2\sqrt{2}\)
\(\Rightarrow d\left(M;\Delta\right)_{max}=R+d\left(I;\Delta\right)=\sqrt{2}+2\sqrt{2}=3\sqrt{2}\)
16 tháng 8 2023
12:
a: Gọi M là trung điểm của BC
trên tia đối của tia MA, lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hình chữ nhật
=>\(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\)
=>\(\overrightarrow{v}=\overrightarrow{AD}\)
b: \(\left|\overrightarrow{v}\right|=\left|\overrightarrow{AD}\right|=AD=2\cdot AM=2\cdot\dfrac{BC}{2}=BC=\sqrt{\left(6a\right)^2+\left(8a\right)^2}=10a\)
16 tháng 8 2023
hình như đó đâu phải là câu 12 đâu ạ 🤔🤔🤔 trong đề câu 12 có chi tiết nào liên quan tới M đâu 🤔
CD
0
CD
0
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2022
\(sina.sinb=-\dfrac{1}{2}\left[cos\left(a+b\right)-cos\left(a-b\right)\right]\) là công thức đúng
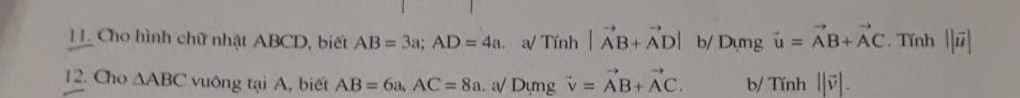
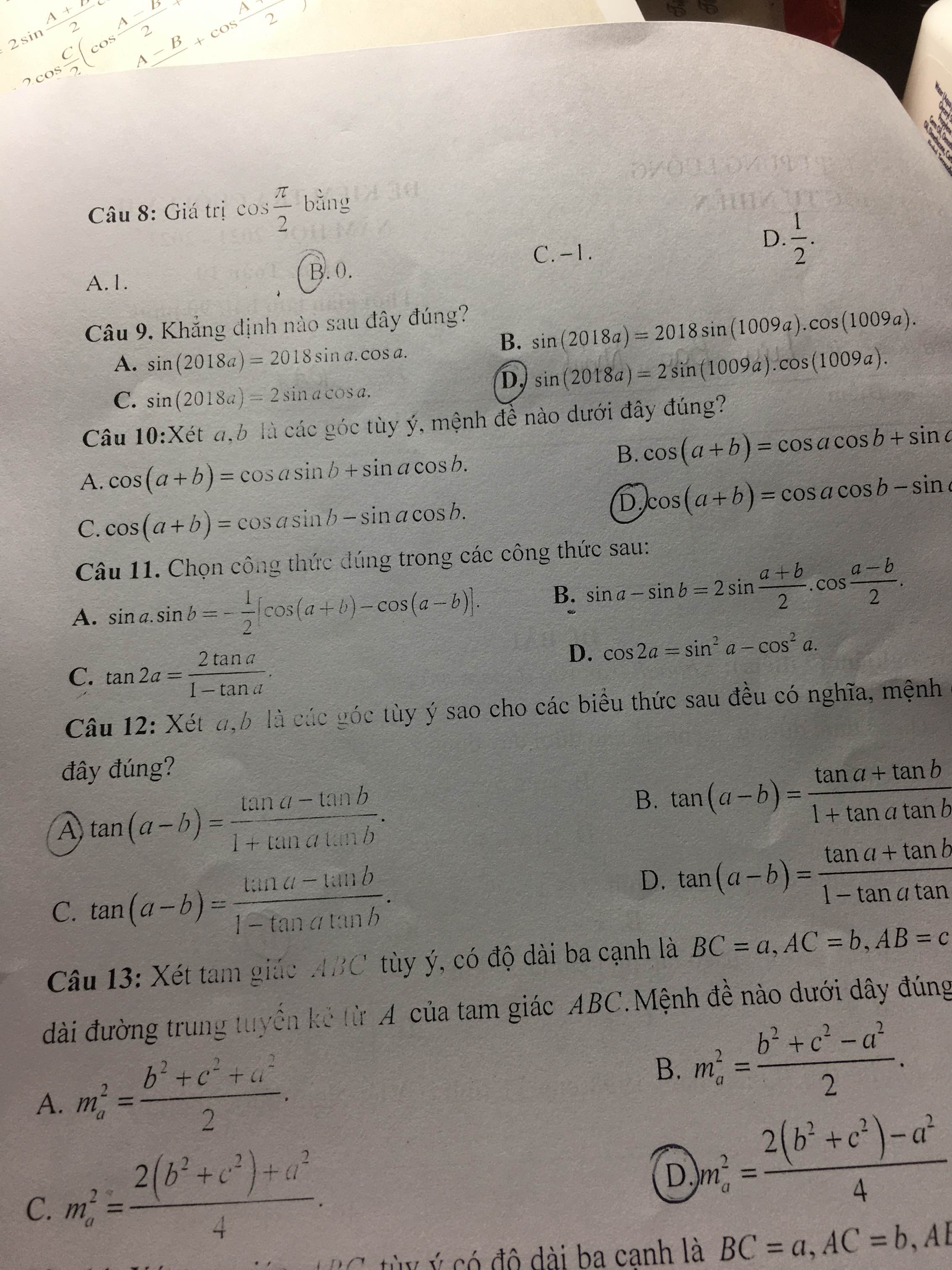
11.
\(BPT\Leftrightarrow\left\{{}\begin{matrix}3-x>0\\\left|1-x\right|>x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< 3\\\left|x-1\right|>x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< 3\\x-1< 0\end{matrix}\right.\) \(\Leftrightarrow x< 1\)
Đáp án A
12.
Đường thằng d nhận (1;2) là 1 vtpt nên đường thẳng vuông góc d nhận (2;-1) là 1 vtpt
\(\Rightarrow\) Loại A, C
Với đáp án B, đường thẳng cắt 2 trục tại \(A\left(0;-1\right)\) và \(B\left(\dfrac{1}{2};0\right)\)
\(S_{OAB}=\dfrac{1}{2}.1.\left(\dfrac{1}{2}\right)=\dfrac{1}{4}\ne1\) (ktm)
Vậy D là đáp án đúng