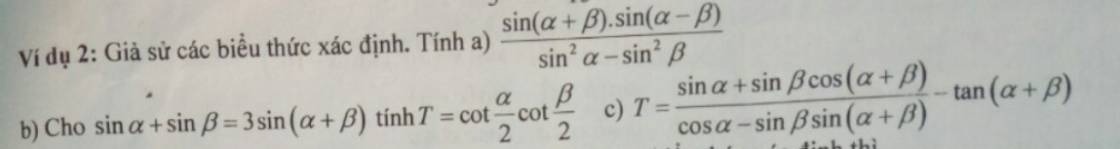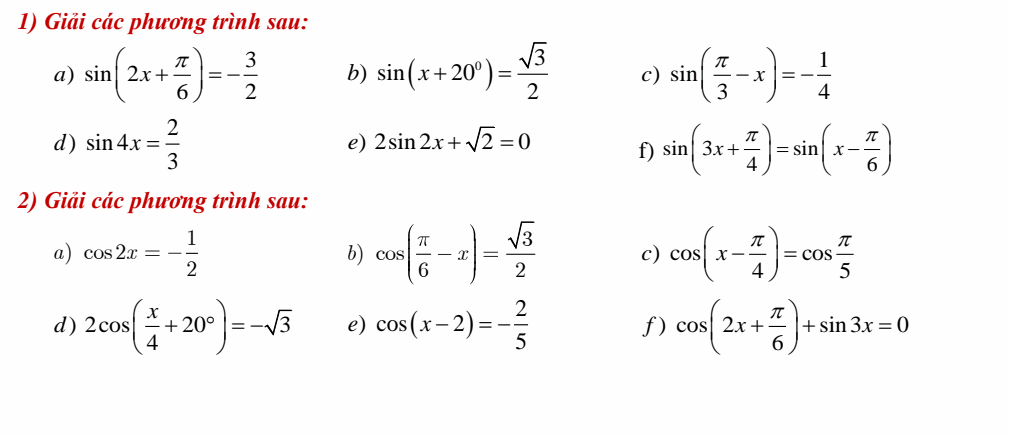Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



4.
\(\lim\limits_{x\rightarrow8}f\left(x\right)=\lim\limits_{x\rightarrow8}\dfrac{\sqrt[3]{x}-2}{x-8}=\lim\limits_{x\rightarrow8}\dfrac{x-8}{\left(x-8\right)\left(\sqrt[3]{x^2}+2\sqrt[3]{x}+4\right)}=\lim\limits_{x\rightarrow8}\dfrac{1}{\sqrt[3]{x^2}+2\sqrt[3]{x}+4}\)
\(=\dfrac{1}{4+4+4}=\dfrac{1}{12}\)
\(f\left(8\right)=3.8-20=4\)
\(\Rightarrow\lim\limits_{x\rightarrow8}f\left(x\right)\ne f\left(8\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=8\)
5.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{1+2x}-1+1-\sqrt[3]{1+3x}}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{2x}{\sqrt[]{1+2x}+1}-\dfrac{3x}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{2}{\sqrt[]{1+2x}+1}-\dfrac{3}{1+\sqrt[3]{1+3x}+\sqrt[3]{\left(1+3x\right)^2}}\right)=\dfrac{2}{1+1}-\dfrac{3}{1+1+1}=0\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(3x^2-2x\right)=0\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=f\left(0\right)\)
\(\Rightarrow\) Hàm liên tục tại \(x=0\)
6.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\sqrt[3]{6x+1}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[]{4x+1}-\left(2x+1\right)+\left(2x+1-\sqrt[3]{6x+1}\right)}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\dfrac{-x^2}{\sqrt[]{4x+1}+2x+1}+\dfrac{x^2\left(8x+12\right)}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}}{x^2}\)
\(=\lim\limits_{x\rightarrow0^+}\left(\dfrac{-1}{\sqrt[]{4x+1}+2x+1}+\dfrac{8x+12}{\left(2x+1\right)^2+\left(2x+1\right)\sqrt[3]{6x+1}+\sqrt[3]{\left(6x+1\right)^2}}\right)\)
\(=\dfrac{-1}{1+1}+\dfrac{12}{1+1+1}=\dfrac{7}{2}\)
\(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(2-3x\right)=2\)
\(\Rightarrow\lim\limits_{x\rightarrow0^+}f\left(x\right)\ne\lim\limits_{x\rightarrow0^-}f\left(x\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)

a: \(=\dfrac{-\dfrac{1}{2}\left[cos\left(a+b+a-b\right)-cos\left(a+b-a+b\right)\right]}{cos^2b-cos^2a}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left[cos2a-cos2b\right]}{\dfrac{1-cos2b}{2}-\dfrac{1-cos2a}{2}}\)
\(=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1-cos2b-1+cos2a}{2}}=\dfrac{-\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}{\dfrac{1}{2}\cdot\left(cos2a-cos2b\right)}=-1\)
c: \(T=\dfrac{sina+sinb\cdot\left(cosa\cdot cosb-sina\cdot sinb\right)}{cosa-sinb\cdot\left(sina\cdot cosb+sinb\cdot cosa\right)}-tan\left(a+b\right)\)
\(=\dfrac{sina+sinb\cdot cosa\cdot cosb-sin^2b\cdot sina}{cosa-sinb\cdot sina\cdot cosb-sin^2b\cdot cosa}-tan\left(a+b\right)\)
\(=\dfrac{sina\left(1-sin^2b\right)+sinb\cdot cosa\cdot cosb}{cosa\left(1-sin^2b\right)-sinb\cdot sina\cdot cosb}\)-tan(a+b)
\(=\dfrac{sina\cdot cos^2b+sinb\cdot cosa\cdot cosb}{cosa\cdot cos^2b-sinb\cdot sina\cdot cosb}-tan\left(a+b\right)\)
\(=\dfrac{sina\cdot cosb+sinb\cdot cosa}{cosa\cdot cosb-sina\cdot sinb}-tan\left(a+b\right)\)
\(=\dfrac{sin\left(a+b\right)}{cos\left(a+b\right)}-tan\left(a+b\right)=0\)

1.
\(-1\le sin\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow1\le y\le5\)
\(y_{min}=1\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=-1\)
\(y_{max}=5\) khi \(sin\left(x-\dfrac{\pi}{2}\right)=1\)
2.
\(-1\le cos2x\le1\Rightarrow\dfrac{5}{2}\le y\le\dfrac{7}{2}\)
\(y_{min}=\dfrac{5}{2}\) khi \(cos2x=1\)
\(y_{max}=\dfrac{7}{2}\) khi \(cos2x=-1\)
3.
\(0\le cos^2\left(2x+\dfrac{\pi}{3}\right)\le1\Rightarrow-2\le y\le-1\)
\(y_{min}=-2\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=\pm1\)
\(y_{max}=-1\) khi \(cos\left(2x+\dfrac{\pi}{3}\right)=0\)
4.
\(-1\le cos\left(4x^2\right)\le1\Rightarrow-2\le y\le\sqrt{2}-2\)
\(y_{min}=-1\) khi \(cos\left(4x^2\right)=-1\)
\(y_{max}=\sqrt{2}-2\) khi \(cos\left(4x^2\right)=1\)

1.
c, \(sin\left(\dfrac{\pi}{3}-x\right)=-\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{3}-x=arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\\dfrac{\pi}{3}-x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}-arcsin\left(-\dfrac{1}{4}\right)+k.360^o\\x=-\dfrac{2\pi}{3}+arcsin\left(-\dfrac{1}{4}\right)+k.360^o\end{matrix}\right.\)
d, \(sin4x=\dfrac{2}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=arcsin\dfrac{2}{3}+k2\pi\\4x=\pi-arcsin\dfrac{2}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arcsin\dfrac{2}{3}+\dfrac{k\pi}{2}\end{matrix}\right.\)
1.
e, \(2sin2x+\sqrt{2}=0\)
\(\Leftrightarrow sin2x=-\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin2x=sin\left(-\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{8}+k\pi\\x=\dfrac{5\pi}{8}+k\pi\end{matrix}\right.\)

EG là đường trung bình tam giác MNP \(\Rightarrow\left\{{}\begin{matrix}EG||MN\\EG=\dfrac{1}{2}MN=x\end{matrix}\right.\)
FG là đường trung bình tam giác MPQ \(\Rightarrow\left\{{}\begin{matrix}FG=\dfrac{1}{2}PQ=x\sqrt{2}\\FG||PQ\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=\widehat{\left(EG;FG\right)}\)
\(cos\widehat{EGF}=\dfrac{EG^2+FG^2-EF^2}{2EG.FG}=-\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{EGF}=135^0\)
\(\Rightarrow\widehat{\left(MN;PQ\right)}=180^0-135^0=45^0\)

1 xào đc \(40:1800\times150=\dfrac{10}{3}\approx3,33\left(triệu\right)\)

\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{\pi}{4}+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất là \(x=\dfrac{\pi}{4}\approx0.79\)
Đáp án C

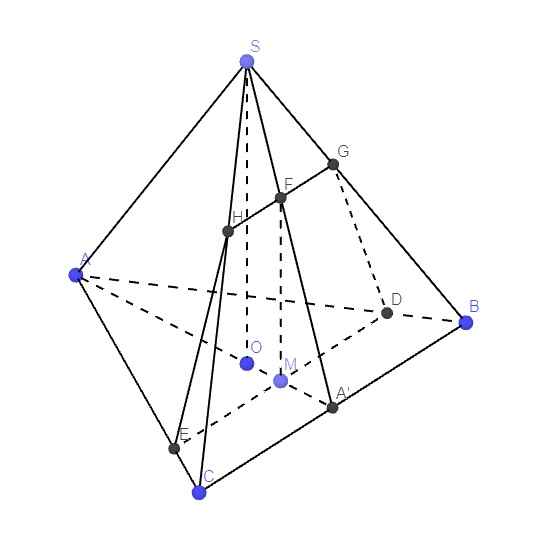
\(\left\{{}\begin{matrix}SO\perp BC\\SO\perp CA\end{matrix}\right.\) \(\Rightarrow SO\perp\left(ABC\right)\)
\(AA'=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow AO=\dfrac{2}{3}AA'=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow M\) nằm trên đoạn thẳng OA'
Qua M kẻ đường thẳng song song BC cắt AB và AC lần lượt tại D và E
Trong mp (SAA'), qua M kẻ đường thẳng song song SO cắt SA' tại F
Trong mp (SBC), qua F kẻ đường thẳng song song BC cắt SB và SC lần lượt tại G và H
\(\Rightarrow\) Hình thang DEHG là thiết diện của (P) và chóp
\(FM||SO\Rightarrow FM\perp\left(ABC\right)\Rightarrow FM\perp ED\)
Áp dụng định lý Talet cho tam giác ABC:
\(\dfrac{DE}{BC}=\dfrac{AM}{AA'}\Rightarrow DE=\dfrac{BC.AM}{AA'}=\dfrac{a.x}{\dfrac{a\sqrt{3}}{2}}=\dfrac{2x\sqrt{3}}{3}\)
Talet tam giác SOA':
\(\dfrac{FM}{SO}=\dfrac{MA'}{OA'}\Rightarrow FM=\dfrac{SO.MA'}{OA'}=\dfrac{2a.\left(\dfrac{a\sqrt{3}}{2}-x\right)}{\dfrac{a\sqrt{3}}{6}}=6a-4\sqrt{3}x\)
Talet tam giác SBC:
\(\dfrac{GH}{BC}=\dfrac{SF}{SA'}=1-\dfrac{FA'}{SA'}=1-\dfrac{FM}{SO}=1-\dfrac{6a-4\sqrt{3}x}{2a}=\dfrac{2\sqrt{3}x-2a}{a}\)
\(\Rightarrow GH=2\sqrt{3}x-2a\)
\(S_{DEHG}=\dfrac{1}{2}\left(DE+GH\right).FM=\dfrac{1}{2}\left(\dfrac{2x\sqrt{3}}{3}+2\sqrt{3}x-2a\right)\left(6a-4\sqrt{3}x\right)\)
\(=\dfrac{1}{3}\left(4\sqrt{3}x-3a\right)\left(6a-4\sqrt{3}x\right)\le\dfrac{1}{12}\left(4\sqrt{3}x-3a+6a-4\sqrt{3}x\right)^2=\dfrac{9a^2}{12}\)
Dấu "=" xảy ra khi \(4\sqrt{3}x-3a=6a-4\sqrt{3}x\Leftrightarrow x=\dfrac{9a}{8\sqrt{3}}=\dfrac{3a\sqrt{3}}{8}\)