
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
Để pt có 2 nghiê pb thì:
$\Delta'=1-(m-3)>0\Leftrightarrow m< 4$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=m-3\end{matrix}\right.\)
Khi đó:
\(x_1^2-2x_2+x_1x_2=-12\)
\(\Leftrightarrow x_1^2-2(2-x_1)+x_1(2-x_1)=-12\)
\(\Leftrightarrow x_1=-2\Leftrightarrow x_2=2-x_1=4\)
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)

\(x+2y=8\Leftrightarrow x=8-2y\Rightarrow B=xy=\left(8-2y\right)y=-2\left(y^2-4y+4\right)+8=-2\left(y-2\right)^2+8\le8.\)
B max = 8 khi y =2 ; x = 4 .

\(x+y=1\Rightarrow x=1-y\)
\(C=x^2+y^2+xy=\left(1-y\right)^2+y^2+\left(1-y\right)y\)
\(=y^2-y+1\)\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)
=>minC=\(\dfrac{3}{4}\) \(\Leftrightarrow y=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{2}\)
Ta có :
\(x+y=1\Rightarrow\left(x+y\right)^2=1\)
\(\Leftrightarrow x^2+2xy+y^2=1\)
\(\Leftrightarrow x^2+xy+y^2=1-xy\ge1-\left(\dfrac{x+y}{2}\right)^2=1-\dfrac{1}{4}=\dfrac{3}{4}\)
Hay \(C \ge \dfrac{3}{4}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

\(\left[3\left(x-1\right)^2+6\right]\left(3+6\right)\ge\left[3\left(x-1\right)+6\right]^2\)
\(\Leftrightarrow3x^2-6x+9\ge x+5\)
\(\Rightarrow A\ge x^4-8x^2+2024=\left(x^2-4\right)^2+2008\ge2008\)
Dấu "=" xảy ra khi \(x=2\)
Có phát hiện ra lỗi sai trong bài làm trên ko? :D

\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1+2\sqrt{x}}\)
\(=\dfrac{x-1}{x-1+2\sqrt{x}}\)
Để \(P>0\)
\(\Rightarrow\dfrac{x-1}{x-1+2\sqrt{x}}>0\)
\(TH_1:x-1>0\Leftrightarrow x>1\)
\(TH_2:x-1+2\sqrt{x}>0\Leftrightarrow\left(\sqrt{x}+1\right)^2< 2\)
\(\Leftrightarrow-\sqrt{2}-1< \sqrt{x}< \sqrt{2}-1\)
\(\Leftrightarrow0< x< 3-2\sqrt{2}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}\left(x-1\right)}{x+2\sqrt{x}-1}\)
\(=\dfrac{\left(x-1\right)\left(\sqrt{x}+1\right)}{x+2\sqrt{x}-1}\)
Để P>0 thì (x-1)/(x+2căn x-1)>0
TH1: x-1>0 và x+2căn x-1>0
=>x>1
TH2: x-1<0 và x+2căn x-1<0
=>0<x<1 và (căn x+1)^2<2
=>0<x<1và \(-\sqrt{2}< \sqrt{x}+1< \sqrt{2}\)
=>\(\left\{{}\begin{matrix}0< x< 1\\-\sqrt{2}-1< \sqrt{x}< \sqrt{2}-1\end{matrix}\right.\Leftrightarrow0< x< 3-2\sqrt{2}\)

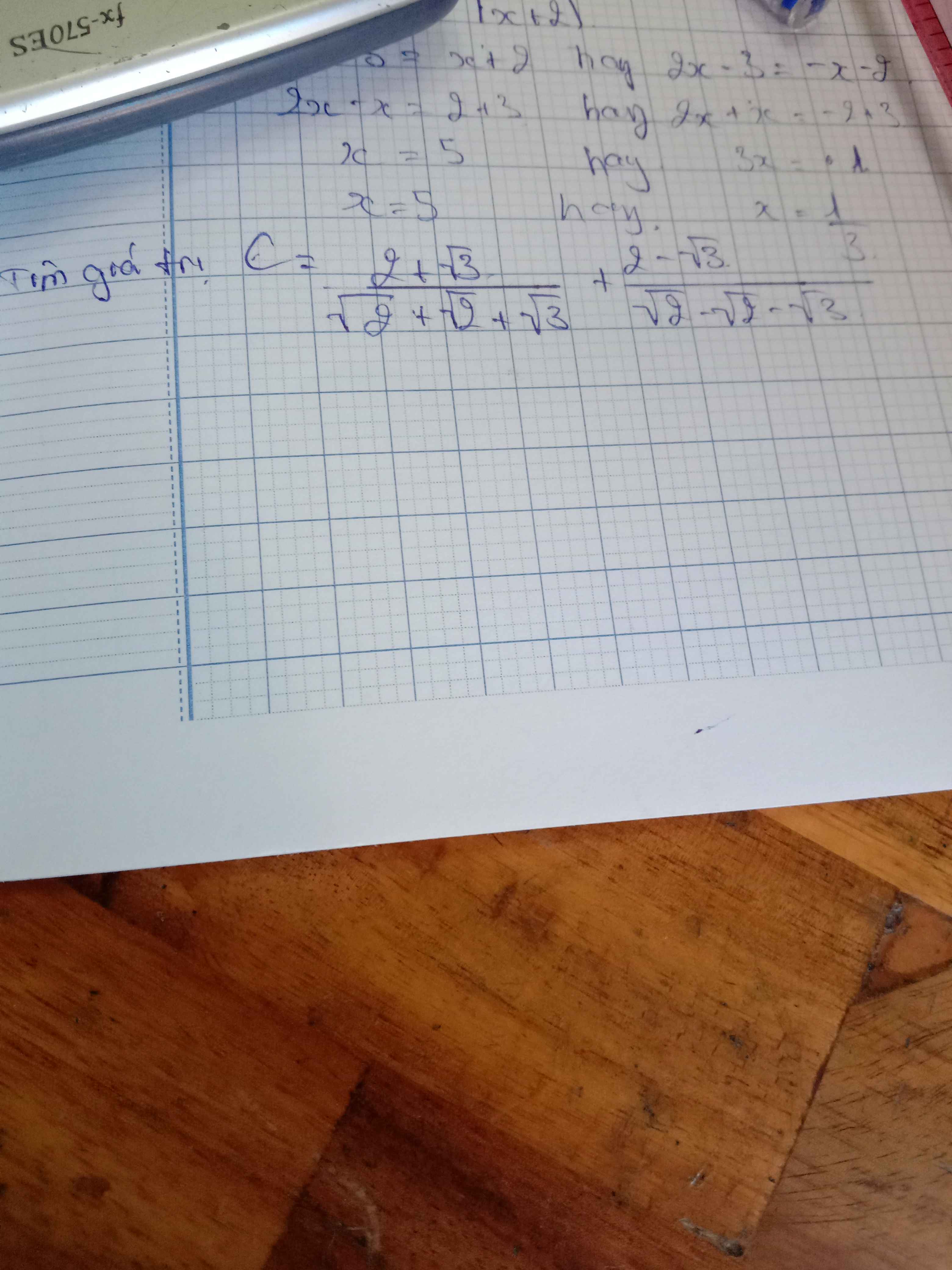

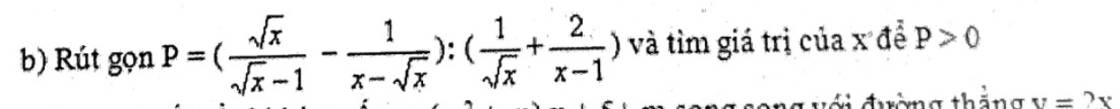 Tìm giúp em giá trị của x ạ. E xin cảm ơn
Tìm giúp em giá trị của x ạ. E xin cảm ơn