
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


8.
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2+2x+3}=a>0\\\sqrt{x^2+4x+5}=b>0\end{matrix}\right.\) \(\Rightarrow2a^2-b^2=x^2+1\)
Pt trở thành:
\(\sqrt{2a^2-b^2}+2a=3b\)
\(\Leftrightarrow\sqrt{2a^2-b^2}=3b-2a\)
\(\Rightarrow2a^2-b^2=4a^2-12ab+9b^2\)
\(\Leftrightarrow2a^2-12ab+10b^2=0\Rightarrow\left[{}\begin{matrix}a=b\\a=5b\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x^2+2x+3}=\sqrt{x^2+4x+5}\\\sqrt{x^2+2x+3}=5\sqrt{x^2+4x+5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+2x+3=x^2+4x+5\\x^2+2x+3=25\left(x^2+4x+5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\24x^2+98x+122=0\left(vn\right)\end{matrix}\right.\)
9.
ĐKXĐ: \(-1\le x\le1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{1+x}=a\ge0\\\sqrt{1-x}=b\ge0\end{matrix}\right.\) \(\Rightarrow a^2+2b^2=3-x=-\left(x-3\right)\)
Pt trở thành:
\(a-2b-3ab=-\left(a^2+2b^2\right)\)
\(\Leftrightarrow a-2b+a^2-3ab+2b^2=0\)
\(\Leftrightarrow a-2b+\left(a-b\right)\left(a-2b\right)=0\)
\(\Leftrightarrow\left(a-2b\right)\left(a-b+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2b\\a+1=b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{1+x}=2\sqrt{1-x}\\\sqrt{1+x}+1=\sqrt{1-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}1+x=4\left(1-x\right)\\x+2+2\sqrt{1+x}=1-x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=3\Rightarrow x=\dfrac{3}{5}\\-1-2x=2\sqrt{1+x}\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow\left\{{}\begin{matrix}-1-2x\ge0\\\left(-1-2x\right)^2=4\left(1+x\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\x^2=\dfrac{3}{4}\end{matrix}\right.\) \(\Rightarrow x=-\dfrac{\sqrt{3}}{2}\)
Vậy \(x=\left\{\dfrac{3}{5};-\dfrac{\sqrt{3}}{2}\right\}\)

5.
Tọa độ dỉnh của (P) là: \(I\left(-\dfrac{b}{2a};\dfrac{-\Delta}{4a}\right)\Rightarrow I\left(1;-4m-2\right)\)
Để I thuộc \(y=3x-1\)
\(\Rightarrow-4m-2=3.1-1\)
\(\Rightarrow m=-1\)
6.a.
Với \(a\ne0\)
\(\left\{{}\begin{matrix}64a+8b+c=0\\-\dfrac{b}{2a}=5\\\dfrac{4ac-b^2}{4a}=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}64a+8b+c=0\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-64a-8b=-64a-8\left(-10a\right)=16a\\b=-10a\\4ac-b^2=48a\end{matrix}\right.\)
\(\Rightarrow4a.16a-\left(-10a\right)^2=48a\)
\(\Rightarrow a=-\dfrac{4}{3}\Rightarrow b=\dfrac{40}{3}\Rightarrow c=-\dfrac{64}{3}\)
Hay pt (P): \(y=-\dfrac{4}{3}x^2+\dfrac{40}{3}x-\dfrac{64}{3}\)
b.
Thay tọa độ 3 điểm vào pt (P) ta được:
\(\left\{{}\begin{matrix}c=-1\\a+b+c=-1\\a-b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-1\\c=-1\end{matrix}\right.\)
Pt (P): \(y=x^2-x-1\)
c.
Do (P) đi qua 3 điểm có tọa độ (1;16); (-1;0); (5;0) nên ta có:
\(\left\{{}\begin{matrix}a+b+c=16\\a-b+c=0\\25a+5b+c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=8\\c=10\end{matrix}\right.\)
hay pt (P) có dạng: \(y=-2x^2+8x+10\)

\(A=\left(m-2;6\right),B=\left(-2;2m+2\right).\)
Để \(A,B\ne\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m-2\ge-2\\2m+2>6\end{cases}}\Rightarrow\orbr{\begin{cases}m\ge0\\m>2\end{cases}}\)
Kết hợp ĐK \(2< m< 8\)
\(\Rightarrow m\in\left(2;8\right)\)

a) \(B\subset A\)
\(\Rightarrow\left(-4;5\right)\subset\left(2m-1;m+3\right)\)
\(\Rightarrow2m-1\le-4< 5\le m+3\)
\(\Rightarrow\hept{\begin{cases}2m-1\ge4\\5\le m+3\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}m< -\frac{3}{2}\\m\ge2\end{cases}}\left(ktm\right)\)
\(\Rightarrow m\in\varnothing\)
b) \(A\text{∩ }B=\varnothing\)
\(\Rightarrow\orbr{\begin{cases}m+3< -4\\5< 2m-1\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}m< -7\\m>3\end{cases}}\)
Vậy \(m< -7;m>3\)

a ) \mathbb{R} \backslash (-3; \, 1]R\(−3;1]=(-∞;-3]∪(1;+∞)
b) (-\infty; \, 1) \backslash [-2; \, 0](−∞;1)\[−2;0]=(- (-\infty; \, 1) \backslash [-2; \, 0]∞;-2)∪(0;1)

a) (-\infty ; \, 2) \cap (-1; \, +\infty)(−∞;2)∩(−1;+∞)=(-1;2)
b) (−1;6) ∪ [4;8)=(-1;8]
c) (−∞;−5] ∩(−5;1)={-5}
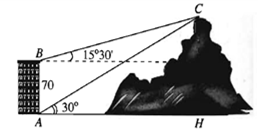
ˆABC=90°+15°30'=105°30'
Xét tam giác ABC có ˆCAB =60°, ˆABC=105°30' ta có:
ˆCAB+ˆABC+ˆACB=180° (định lí tổng ba góc trong tam giác)
⇒ˆACB=180°−ˆCAB−ˆABC
⇒ˆACB=180°−60°−105°30'=14°30'.
Áp dụng định lí sin trong tam giác ABC, ta có: ACsinˆABC=ABsinˆACB
⇒AC=AB.sinˆABCsinˆACB=70.sin105°30'sin14°30'≈269,4(m)


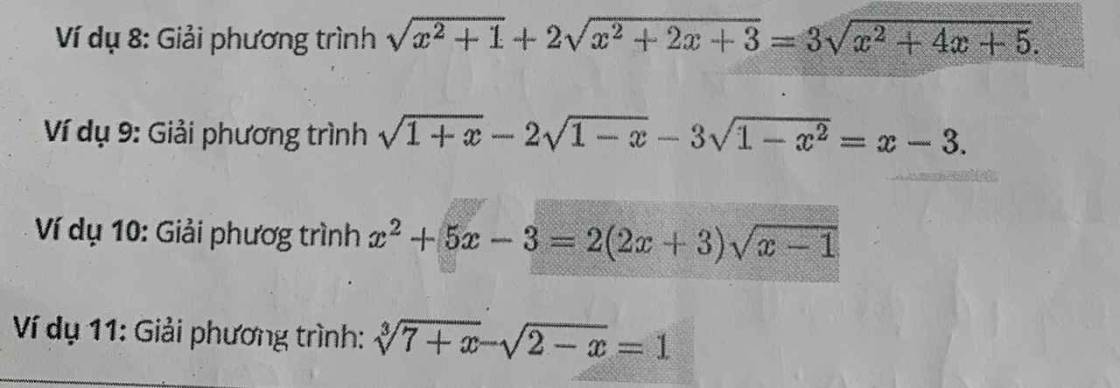


Bài 12:
a: (d): \(\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\)
=>(d) đi qua T(-2;1) và có vecto chỉ phương là (-2;2)
(d')\(\perp\)(d) nên (d') nhận vecto (-2;2) làm vecto pháp tuyến
Phương trình (d') là:
-2(x-3)+2(y-1)=0
=>-(x-3)+(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
b: (d) có vecto chỉ phương là (-2;2)
=>(d) có vecto pháp tuyến là (2;2)=(1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+2+y-1=0
=>x+y+1=0
Tọa độ giao điểm H của (d) và (d') là:
\(\left\{{}\begin{matrix}x+y+1=0\\-x+y+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=-1\\-x+y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-3\\x+y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=-1-x=-1+\dfrac{3}{2}=\dfrac{1}{2}\end{matrix}\right.\)
c: A' đối xứng với A qua d
=>A'A\(\perp\)d
mà d'\(\perp\)d và \(A\in d'\)
nên d' chính là phương trình AA'
=>H là trung điểm của A'A
A(3;1); H(-3/2;1/2); A'(x;y)
H là trung điểm của A'A
=>\(\left\{{}\begin{matrix}x_A+x_{A'}=2\cdot x_H=-3\\y_A+y_{A'}=2\cdot y_H=2\cdot\dfrac{1}{2}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_{A'}+3=-3\\y_A+1=1\end{matrix}\right.\)
=>A'(-6;0)
Bài 13:
a: M(2;-5); N(4;-3)
Tọa độ tâm I là:
\(\left\{{}\begin{matrix}x=\dfrac{2+4}{2}=\dfrac{6}{2}=3\\y=\dfrac{-5+\left(-3\right)}{2}=-\dfrac{8}{2}=-4\end{matrix}\right.\)
I(3;-4); M(2;-5)
\(IM=\sqrt{\left(2-3\right)^2+\left(-5+4\right)^2}=\sqrt{2}\)
Phương trình (C) là:
\(\left(x-3\right)^2+\left(y+4\right)^2=IM^2=2\)
b: (C) có tâm là I(1;-2) và tiếp xúc với đường thẳng 4x-3y+5=0
=>Bán kính là \(R=d\left(I;4x-3y+5=0\right)=\dfrac{\left|1\cdot4+\left(-2\right)\cdot\left(-3\right)+5\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{15}{5}=3\)
Phương trình (C) là:
\(\left(x-1\right)^2+\left(y+2\right)^2=R^2=9\)
c: Gọi phương trình (C) là: \(x^2+y^2+2ax+2by+c=0\)
Thay x=1 và y=0 vào (C), ta được:
\(1^2+0^2+2\cdot a\cdot1+2\cdot b\cdot0+c=0\)
=>2a+c=-1(1)
Thay x=0 và y=-2 vào (C), ta được:
\(0^2+\left(-2\right)^2+2\cdot a\cdot0+2\cdot b\cdot\left(-2\right)+c=0\)
=>4-4b+c=0
=>-4b+c=-4(2)
Thay x=2 và y=3 vào (C), ta được:
\(2^2+3^2+2\cdot a\cdot2+2\cdot b\cdot3+c=0\)
=>4a+6b+c=-13(3)
Từ (1),(2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+c=-1\\-4b+c=-4\\4a+6b+c=-13\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+4b=-1+4=5\\-2a-6b=-1+13=12\\2a+c=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2b=5+12=17\\2a+4b=5\\2a+c=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{17}{2}\\2a=5-4b=5-4\cdot\dfrac{-17}{2}=5+34=39\\2a+c=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=-\dfrac{17}{2}\\a=\dfrac{39}{2}\\c=-1-2a=-1-2\cdot\dfrac{39}{2}=-40\end{matrix}\right.\)
Vậy: (C): \(x^2+y^2+39x-17y-40=0\)