
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được



b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)

\(x+\sqrt{4-x^2}=2\)
\(\Leftrightarrow4-x^2=\left(2-x\right)^2\)
\(\Leftrightarrow4-x^2=4-8x+x^2\)
\(\Leftrightarrow4-x^2-4+8x-x^2=0\)
\(\Leftrightarrow8x-2x^2=0\)
\(\Leftrightarrow2x\left(4-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
\(x+\sqrt{1-x^2}=1\)
\(\Leftrightarrow1-x^2=\left(1-x\right)^2\)
\(\Leftrightarrow1-x^2=1-2x+x^2\)
\(\Leftrightarrow1-x^2-1+2x-x^2=0\)
\(\Leftrightarrow2x-2x^2=0\)
\(\Leftrightarrow2x\left(1-x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=0\\1-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)




a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
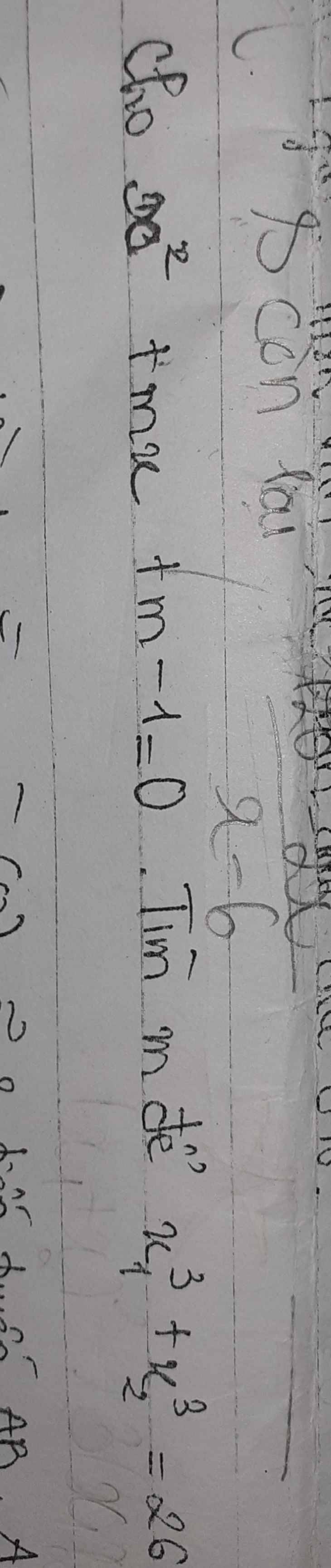

 giúp e với ạ đang cần gấp
giúp e với ạ đang cần gấp
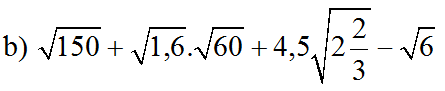


 Giải giúp e vs ạ ,e đang cần gấp
Giải giúp e vs ạ ,e đang cần gấp


\(\text{Δ}=m^2-4\cdot1\cdot\left(m-1\right)\)
\(=m^2-4m+4=\left(m-2\right)^2>=0\forall m\)
=>Phương trình luôn có hai nghiệm
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-m\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
\(x_1^3+x_2^3=26\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=26\)
=>\(\left(-m\right)^3-3\cdot\left(-m\right)\left(m-1\right)=26\)
=>\(-m^3+3m\left(m-1\right)=26\)
=>\(m^3-3m\left(m-1\right)=-26\)
=>\(m^3-3m^2+3m=-26\)
=>\(m^3-3m^2+3m-1=-27\)
=>\(\left(m-1\right)^3=-27\)
=>m-1=-3
=>m=-2