K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DD
2
NM
Nguyễn Minh Quang
Giáo viên
24 tháng 3 2022
hàm số \(y=x^0\text{ cũng chính là đường thẳng }y=1\) đây là một đường thẳng vuông góc với trục Oy tại điểm (0,1) thôi
còn hàm \(y=\frac{1}{x}\Rightarrow y'=-\frac{1}{x^2}< 0\forall x\) nên hàm số nghịch biến trên R.
Đồ thị hàm số
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 11 2021
12. \(\dfrac{4\sqrt{3}}{3}\pi\)
13. \(12\pi\)
14. \(\sqrt{6}\pi a^2\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
\(\int\left(\dfrac{7}{cos^2x}+cosx-3^x+2\right)dx=7tanx+sinx-\dfrac{3^x}{ln3}+2x+C\)
LT
0
TT
1
VA
0
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
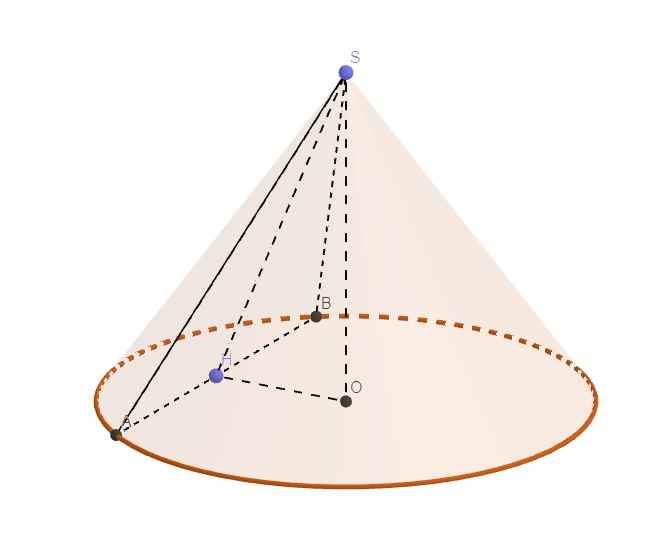
Đặt tên các điểm như hình vẽ, với H là trung điểm AB
\(\Rightarrow\widehat{SHO}=60^0\) (là góc giữa thiết diện và đáy nón)
Tam giác SAB đều \(\Rightarrow SH=\dfrac{AB\sqrt{3}}{2}=2\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow\left\{{}\begin{matrix}OH=SH.cos60^0=\sqrt{3}\\h=SO=SH.sin60^0=3\end{matrix}\right.\)
\(R=OA=\sqrt{AH^2+OH^2}=\sqrt{2^2+3}=\sqrt{7}\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi.7.3=7\pi\left(cm^3\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 6 2021
- Với \(x=2\) chuỗi hiển nhiên hội tụ
- Với \(x\ne2\):
\(u_{n+1}=\dfrac{\left(-1\right)^{n+1}\left(x-2\right)^{2n+2}}{\left(n^2+2n+2\right)4^{n+1}}\)
\(\lim\limits\left|\dfrac{u_{n+1}}{u_n}\right|=\lim\left|\dfrac{\left(-1\right)^{n+1}.\left(x-2\right)^{2n+2}}{\left(n^2+2n+2\right).4^{n+1}}.\dfrac{\left(n^2+1\right)4^n}{\left(-1\right)^n.\left(x-2\right)^{2n}}\right|\)
\(=\left|\dfrac{\left(x-2\right)^2}{4}\right|< 1\)
\(\Rightarrow-2< x-2< 2\Rightarrow0< x< 4\)
- Với \(x=4\) chuỗi trở thành: \(\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n.2^{2n}}{\left(n^2+1\right).4^n}=\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n}{n^2+1}\) hội tụ theo tiêu chuẩn Leibniz
- Với \(x=0\) chuổi trở thành \(\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n}{n^2+1}\) giống như trên hội tụ theo t/c Leibniz
Vậy miền hội tụ của chuỗi là \(x\in\left[0;4\right]\)
1+1=2
1+2=3
1+3=4