K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 10 2021
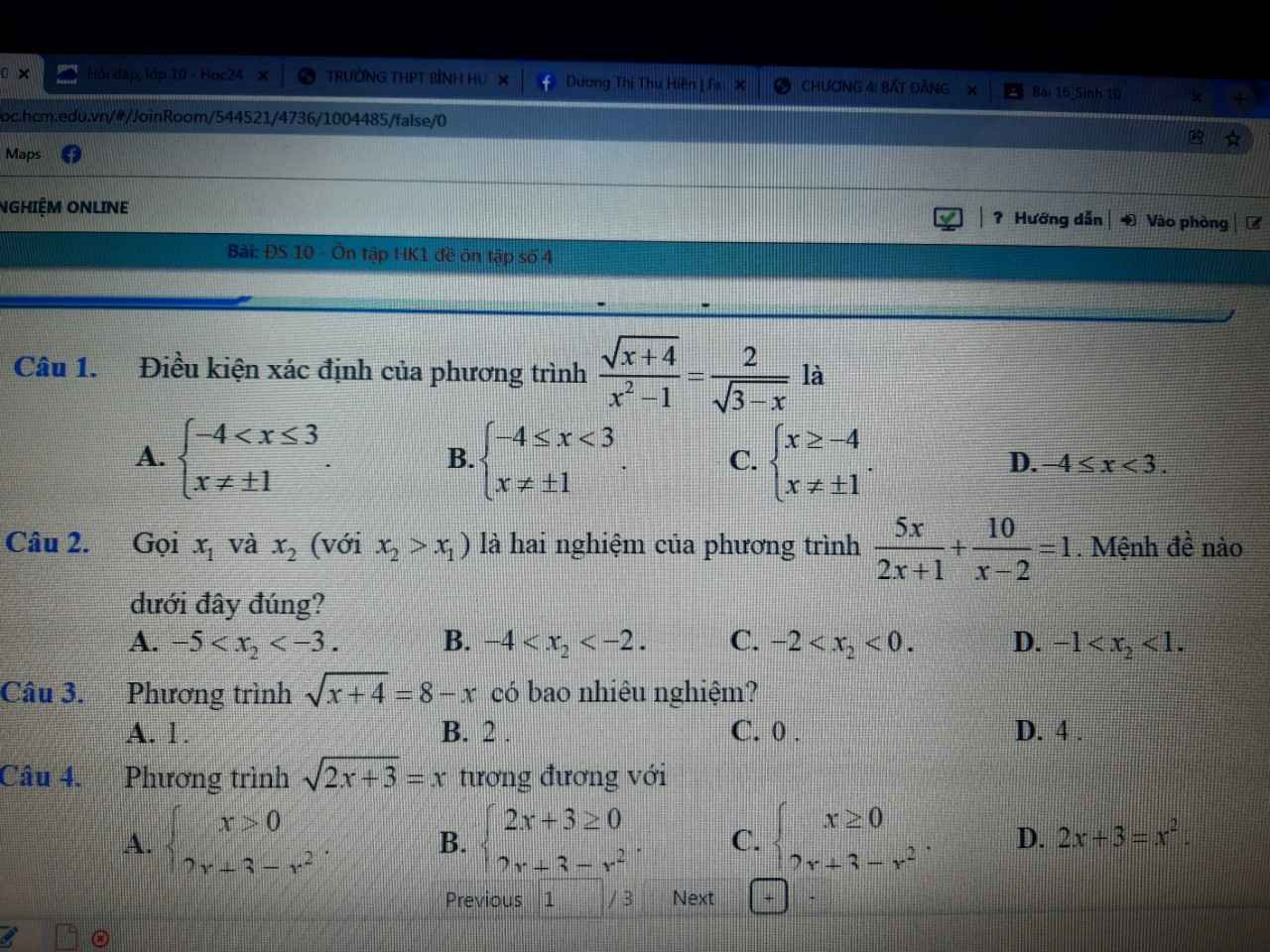
b: ĐKXĐ: \(x\notin\left\{1;-1;-2\right\}\)
d: ĐKXĐ: \(x< 3\)
BC
2
DT
2
8 tháng 11 2021
Bài 6:
Vì \(m^2+1>0\) nên hs nghịch biến trong khoảng \(\left(-\infty;2m\right)\)
8 tháng 11 2021
Bài 3:
6: \(x< 0\) nên \(y=\sqrt[3]{x}\) nghịch biến
HP
29 tháng 3 2021
3.
TH1: \(m=0,pt\Leftrightarrow2x-1=0\Leftrightarrow x=\dfrac{1}{2}\)
TH2: \(m\ne0\)
a, Phương trình có hai nghiệm trái dấu khi \(m\left(4m-1\right)< 0\Leftrightarrow0< m< \dfrac{1}{4}\)
b, Phương trình có hai nghiệm phân biệt khi \(\Delta'=-3m^2-m+1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m< \dfrac{-1-\sqrt{13}}{6}\\m>\dfrac{-1+\sqrt{13}}{6}\end{matrix}\right.\)
c, Phương trình có hai nghiệm dương khi:
\(\left\{{}\begin{matrix}\Delta'>0\\x_1x_2>0\\x_1+x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -\dfrac{1+\sqrt{13}}{6}\\m>1\end{matrix}\right.\)
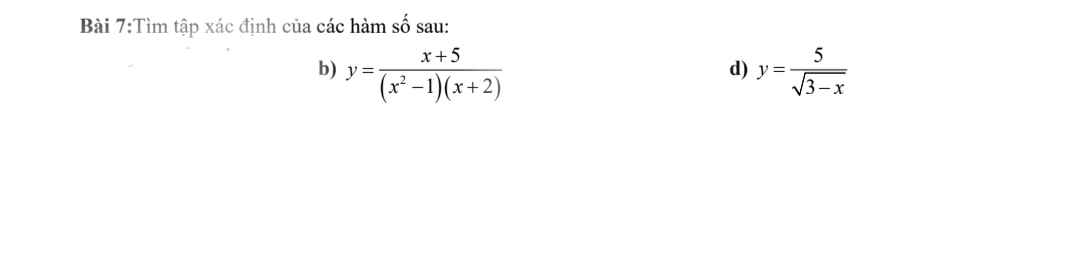
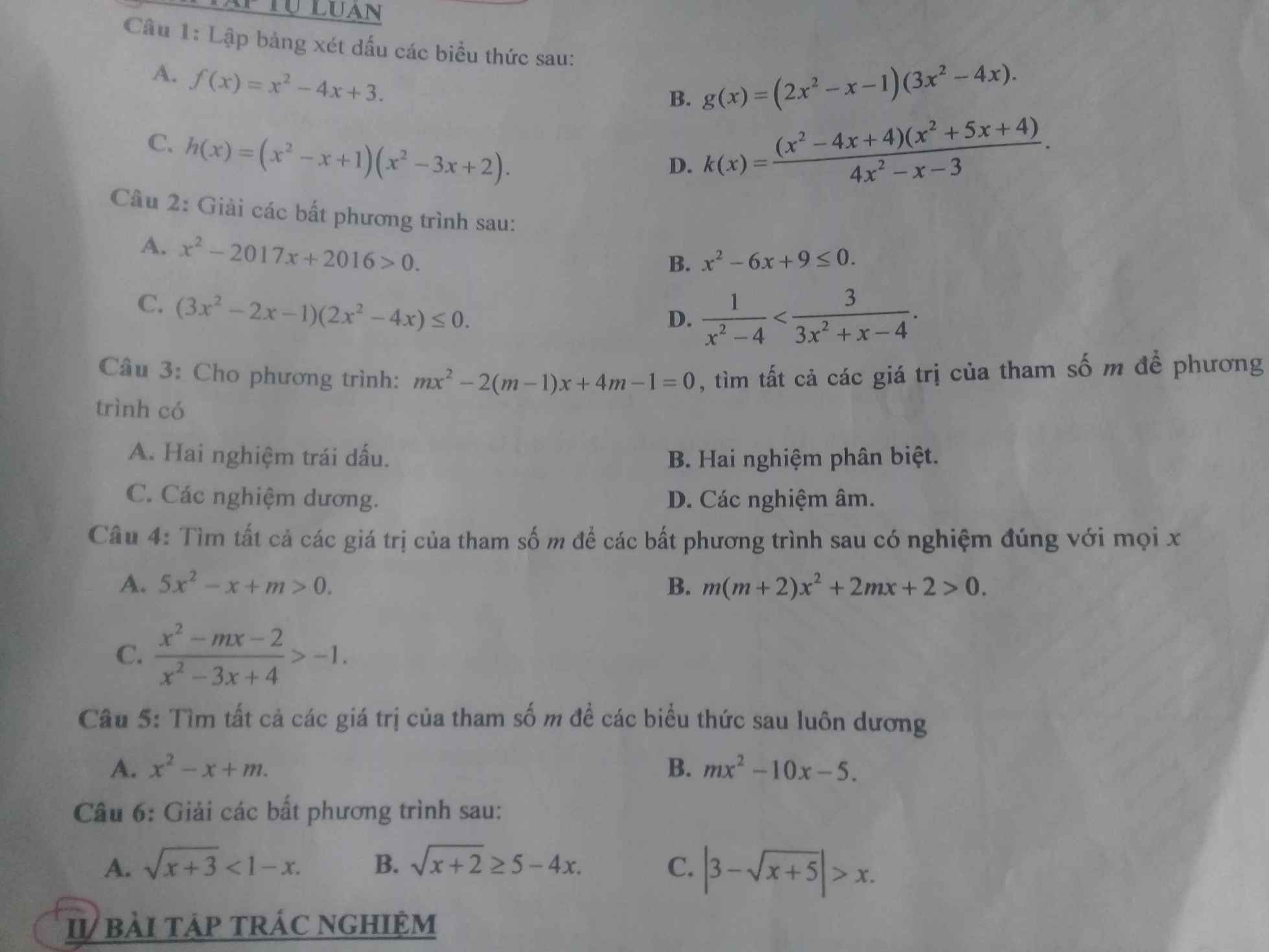
12.1
Giả sử \(G=\left(m;2m-2\right)\left(m\in R\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_H=2x_E-x_G=6-m\\y_H=2y_E-y_G=2-2m\end{matrix}\right.\)
\(\Rightarrow H=\left(6-m;2-2m\right)\)
Mà \(H\in d_2\Rightarrow6-m+2-2m+3=0\Leftrightarrow m=\dfrac{11}{3}\)
\(\Rightarrow G=\left(\dfrac{11}{3};\dfrac{16}{3}\right)\)
\(\Rightarrow\Delta:8x-y-24=0\)
12.2
Giả sử \(A=\left(m;-m-1\right)\left(m\in R\right)\)
Ta có: \(\vec{AM}=\dfrac{1}{3}\vec{MB}\)
\(\Rightarrow\left\{{}\begin{matrix}x_M-x_A=\dfrac{1}{3}\left(x_B-x_M\right)\\y_M-y_A=\dfrac{1}{3}\left(y_B-y_M\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1-m=\dfrac{1}{3}\left(x_B-1\right)\\m+1=\dfrac{1}{3}.y_B\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_B=4-3m\\y_B=3m+3\end{matrix}\right.\)
\(\Rightarrow B=\left(4-3m;3m+3\right)\)
Mà \(B\in d_2\Rightarrow4-3m-2\left(3m+3\right)+2=0\Leftrightarrow m=0\)
\(\Rightarrow A=\left(0;-1\right)\)
\(\Rightarrow d:x-y-1=0\)