Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Lời giải chi tiết:
Theo công thức Anh xtanh ta xác định được vận tốc ban đầu cực đại của electron bứt ra
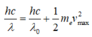
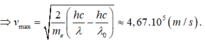
Như vậy theo công thức Anhxtanh thì đó là tốc độ lớn nhất khi bứt ra có nghĩa là tốc độ ban đầu bứt ra của các electron thỏa mãn
![]()
ta có đáp án C.

Hệ thức Anh -xtanh: \(hf = A+ W_{đ max}= A+eU_h\)
Chiếu bức xạ 1:
\(A = hf_1 - \frac{1}{2}m_e.v_{0max}^2= \frac{6,625.10^{-34}.3.10^8}{0,2.10^{-6}}-\frac{1}{2}9,1.10^{-31}.(0,7.10^6)^2= 7,708.10^{-19}J\)
Chiếu bức xạ 2: \(V_{max}= U_h\)
\(hf_2 = A+eU_h= 7,708.10^{-19}+3.1,6.10^{-19}= 1,25.10^{-18}J\)
=> \(\lambda_2 = \frac{hc}{1,25.10^{-18}}= \frac{6,625.10^{-34}.3.10^8}{1,25.10^{-18}}=1,6.10^{-7}m = 0,16 \mu m.\)

Mình hướng dẫn thế này rồi bạn làm tiếp nhé.
a. Áp dụng CT: \(hf=A_t+\dfrac{1}{2}mv^2\)
\(\Rightarrow 6,625.10^{-34}.3.10^8=A_t+\dfrac{1}{2}.9,1.10^{-31}.(0,4.10^6)^2\)
\(\Rightarrow A_t\)
Mà \(A_t=\dfrac{hc}{\lambda_0}\Rightarrow \lambda_0\)
b. Áp dụng: \(\dfrac{hc}{\lambda}=A_t+eV_{max}\)
\(\Rightarrow \lambda\)

Hệ thức Anh -xtanh trong hiện tượng quang điện ngoài
\(\frac{hc}{\lambda} = A+W_{đmax}\)
mà \(\lambda = \lambda_0/2\) => \(\frac{2hc}{\lambda_0} = A+W_{đmax}\)
Lại có \(A = \frac{hc}{\lambda_0}\) => \(W_{đmax}= \frac{2hc}{\lambda_0} -A= 2A - A = A.\)
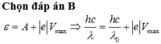
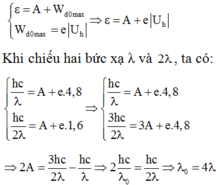
Chọn đáp án C
Theo công thức Anhxtanh ta xác định được vận tốc ban đầu cực đại của electron bức ra
Như vậy theo công thức Anhxtanh thì đó là tốc độ lớn nhất khi bức ra có nghĩa là tốc độ ban đầu bức ra các electron thỏa mãn, ta có đáp án C