Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\left\{{}\begin{matrix}\dfrac{x}{35}-y=2\\y-\dfrac{x}{50}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{x-35y}{35}=2\\\dfrac{50y-x}{50}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-35y=70\\-x+50y=50\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}15y=120\\x-35y=70\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=8\\x=70+35y=70+35\cdot8=350\end{matrix}\right.\)
b: ĐKXĐ: x<>0 và y<>0
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{3}{y}=\dfrac{3}{16}-\dfrac{1}{4}=\dfrac{-1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{2}{48}=\dfrac{1}{24}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\left(nhận\right)\)

ĐKXĐ: x<>0; y<>0
\(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{3}{y}=1\\\dfrac{2}{x}+\dfrac{1}{y}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{3}{y}=1\\\dfrac{6}{x}+\dfrac{3}{y}=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{1}{x}=4\\\dfrac{2}{x}+\dfrac{1}{y}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{4}\\\dfrac{1}{y}=-1-\dfrac{2}{x}=-1-2:\dfrac{-1}{4}=-1+8=7\end{matrix}\right.\)
=>x=-1/4 và y=1/7
ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}a=\dfrac{1}{x}\\b=\dfrac{1}{y}\end{matrix}\right.\)
Hệ phương trình trở thành \(\left\{{}\begin{matrix}5a+3b=1\\2a+b=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=-1-2a\\5a+3\left(-1-2a\right)=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1-2a\\-a-3=1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}a=-4\\b=-1-2.\left(-4\right)\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=-4\\b=7\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}a=\dfrac{1}{x}=-4\\b=\dfrac{1}{y}=7\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{4}\left(tm\right)\\y=\dfrac{1}{7}\left(tm\right)\end{matrix}\right.\)
Vậy HPT có nghiệm \(x=-\dfrac{1}{4}\) và \(y=\dfrac{1}{7}\)

\(\left(x\ne-y;x>\dfrac{y}{2}\right)\Rightarrow\left\{{}\begin{matrix}\dfrac{4}{\sqrt{2x-y}}-\dfrac{21}{x+y}=\dfrac{1}{2}\\\dfrac{3}{\sqrt{2x-y}}+\dfrac{7-\left(x+y\right)}{x+y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{\sqrt{2x-y}}-\dfrac{21}{x+y}=\dfrac{1}{2}\\\dfrac{3}{\sqrt{2x-y}}+\dfrac{7}{x+y}=2\end{matrix}\right.\)
\(đặt:\dfrac{1}{\sqrt{2x-y}}=a>0;\dfrac{1}{x+y}=b\)
\(\Rightarrow\left\{{}\begin{matrix}4a-21b=\dfrac{1}{2}\\3a+7b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\left(tm\right)\\b=\dfrac{1}{14}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{\sqrt{2x-y}}=\dfrac{1}{2}\\\dfrac{1}{x+y}=\dfrac{1}{14}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x-y=4\\x+y=14\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=8\end{matrix}\right.\)(thỏa)

Lời giải:
Đặt $\frac{1}{x-y+2}=a;\frac{1}{x+y-1}=b$ thì HPT trở thành cơ bản:
\(\left\{\begin{matrix}
14a-10b=9\\
3a+2b=4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
14a-10b=9\\
15a+10b=20\end{matrix}\right.\)
$\Rightarrow (14a-10b)+(15a+10b)=9+20$
$\Leftrightarrow 29a=29\Leftrightarrow a=1$.
$b=\frac{4-3a}{2}=\frac{1}{2}$
Vậy: \(\left\{\begin{matrix} \frac{1}{x-y+2}=1\\ \frac{1}{x+y-1}=\frac{1}{2}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x-y+2=1\\ x+y-1=2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x-y=-1\\ x+y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=1\\ y=2\end{matrix}\right.\)

a.
ĐKXĐ: \(x\ne\pm y\)
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+y}=u\\\dfrac{1}{x-y}=v\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u+v=2\\2u+3v=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3u+3v=6\\2u+3v=5\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u=1\\v=2-u\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u=1\\v=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}=1\\\dfrac{1}{x-y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\x-y=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)
b.
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x+7=x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-5x+6=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

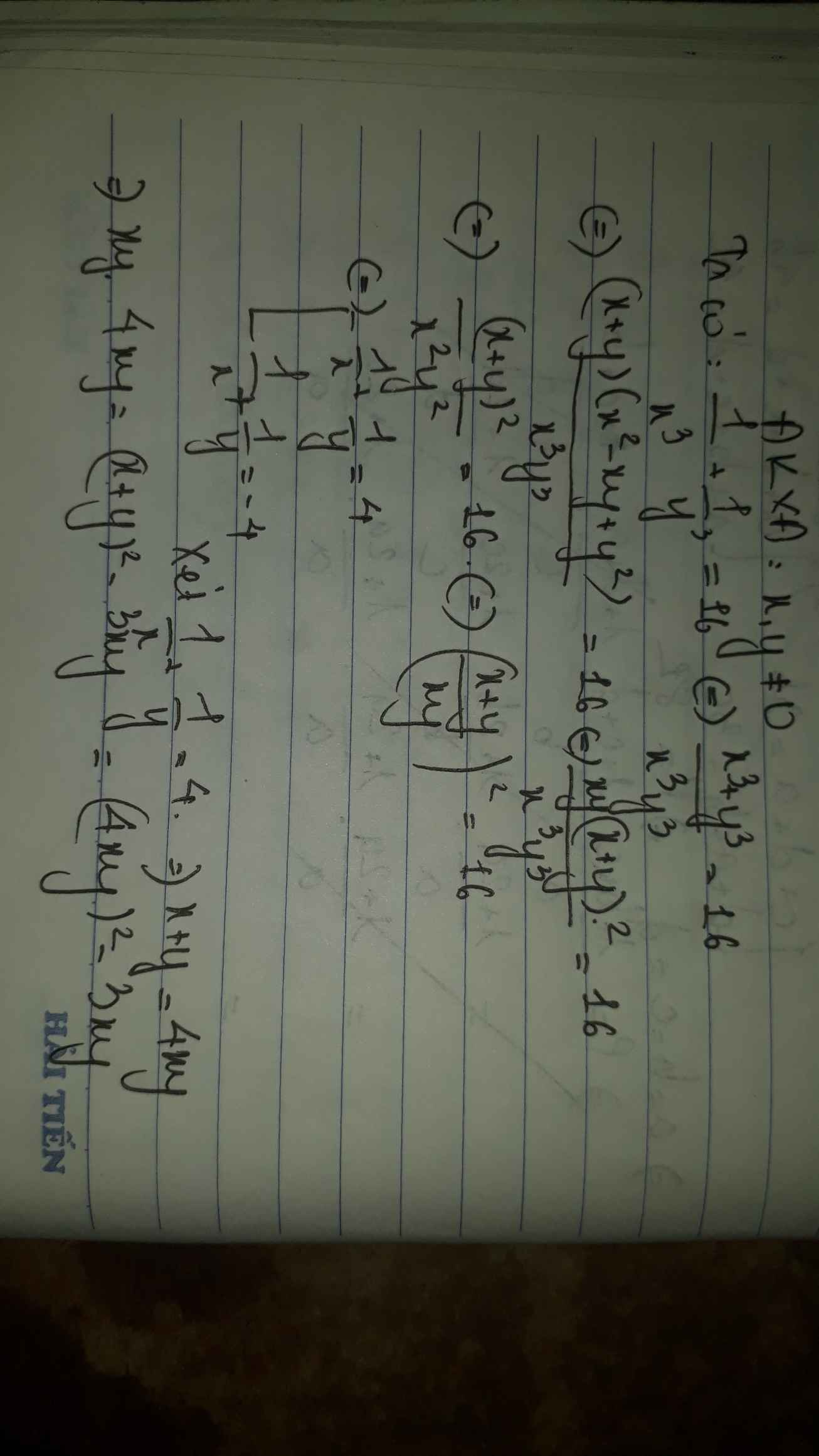
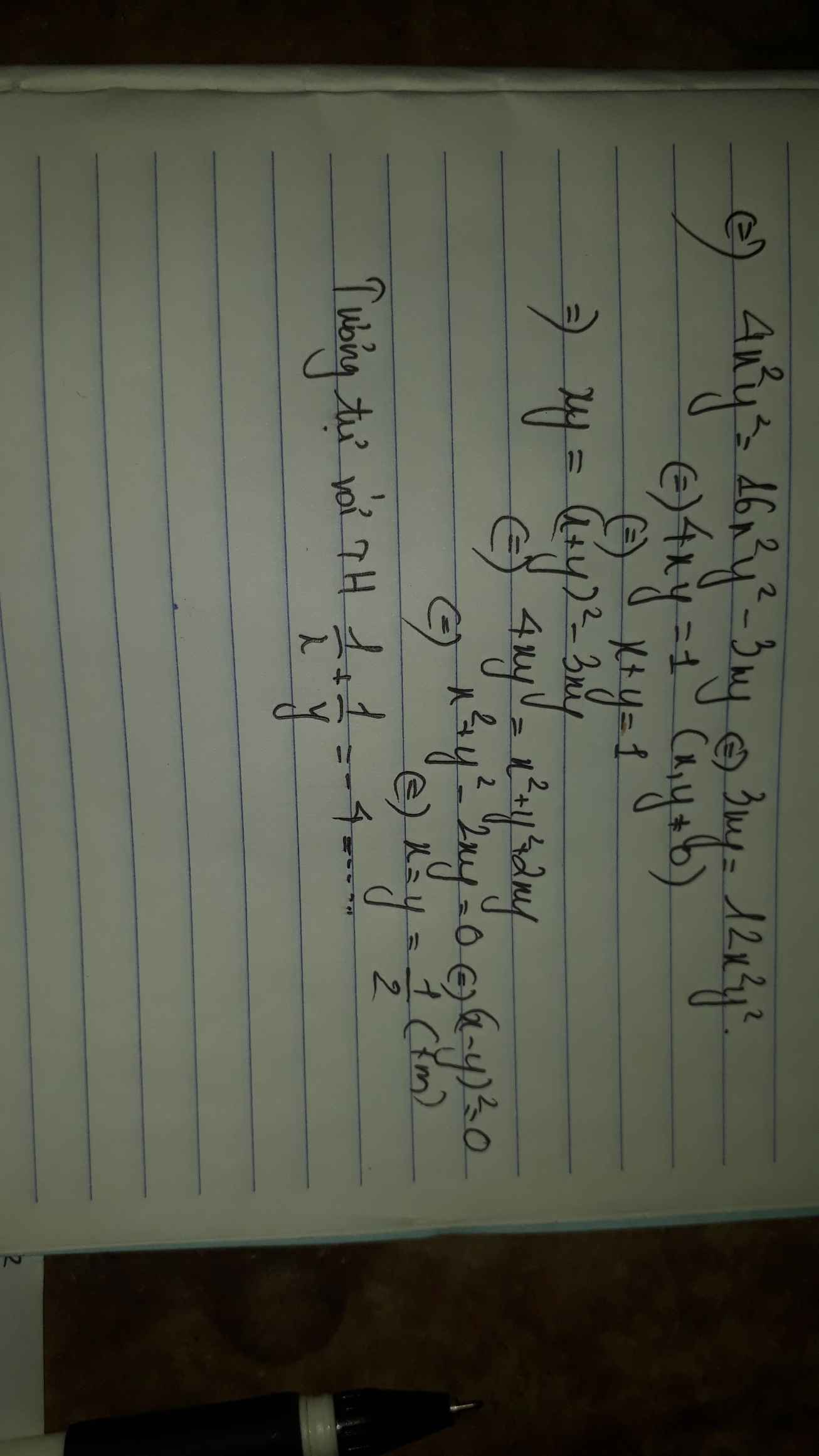

Đặt \(\left[{}\begin{matrix}\dfrac{1}{x}=a\\\dfrac{1}{y}=b\end{matrix}\right.\).
Ta có hệ: \(\left[{}\begin{matrix}a+b=\dfrac{1}{16}\\3a+6b=\dfrac{1}{4}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}a=\dfrac{1}{24}\\b=\dfrac{1}{48}\end{matrix}\right.\)
`=>` \(\left[{}\begin{matrix}x=24\\y=48\end{matrix}\right.\)
Vậy `(x;y)=(24;48)`.