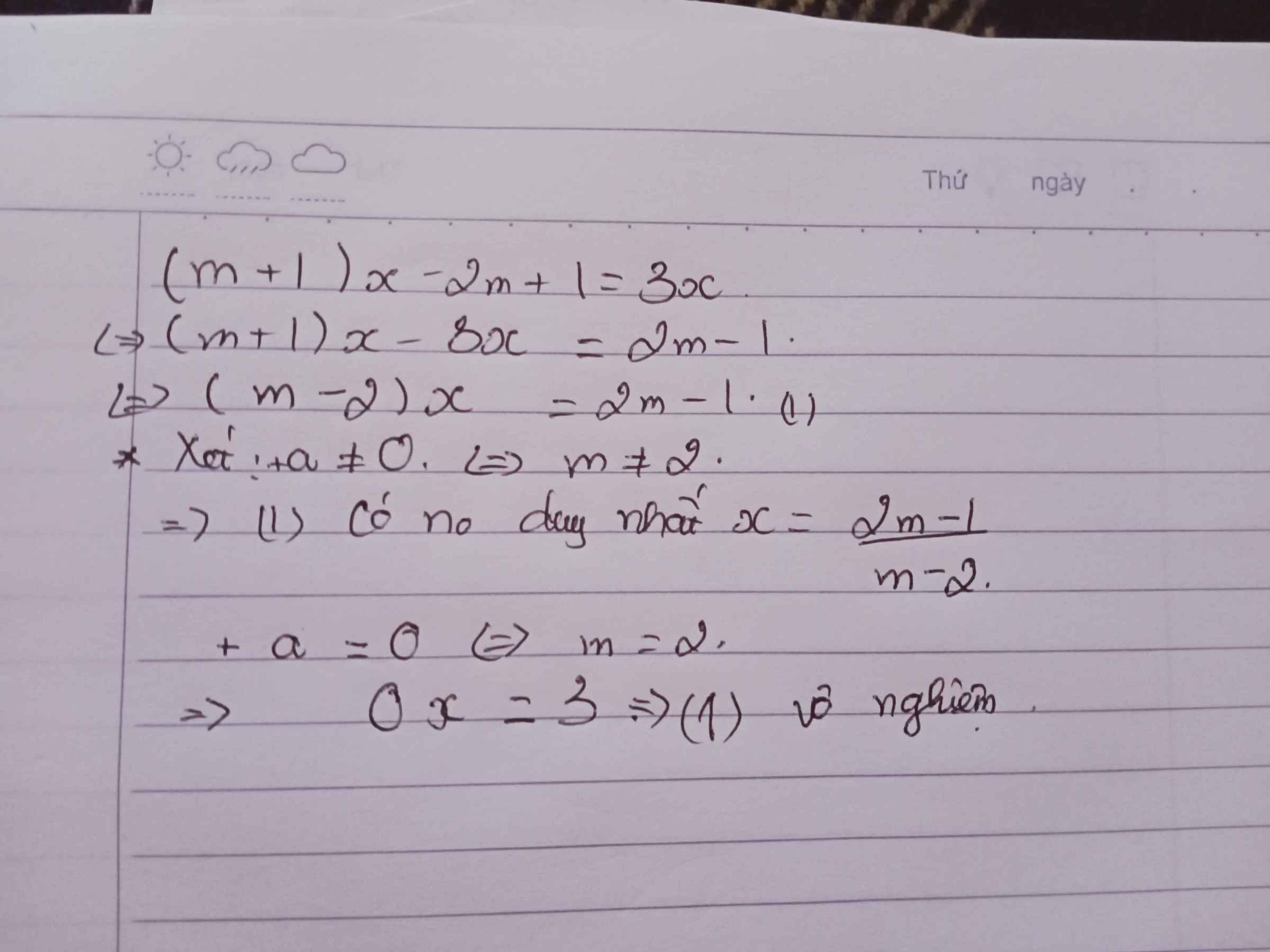TD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
Bài 1: Giải và biện luận các phương trình sau theo tham số m a) 2mx + 3 = m - x b) m(x - 2) = 3x + 1
1
6 tháng 12 2021
b: Để phương trình vô nghiệm thì x-2=0
hay x=2
Để phương trình có nghiệm thì x-2<>0
hay x<>2
BT
1
25 tháng 1 2022
\(\Leftrightarrow-m^2+m+2mx-2=x^2-1\)
\(\Leftrightarrow x^2-1+m^2-m-2mx+2=0\)
\(\Leftrightarrow x^2-2mx+m^2-m+1=0\)
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-m+1\right)\)
=4m-4
Để phương trình có hai nghiệm phân biệt thì 4m-4>0
hay m>1
Để phương trình có nghiệm kép thì 4m-4=0
hay m=1
Để phương trình vô nghiệm thì 4m-4<0
hay m<1
PT
1
CM
29 tháng 11 2019
Phương trình đã cho tương đương với phương trình
(m - 1)(m + 3)x = 4(m - 1)
Với m ≠ 1 và m ≠ -3 phương trình có nghiệm 
Với m = 1 mọi số thực x đều là nghiệm của phương trình;
Với m = -3 phương trình vô nghiệm.
YC
1
DH
20 tháng 11 2019
\(2mx+3=m-x\)
\(\Leftrightarrow x\left(2m+1\right)=m-3\)
+) Nếu \(2m+1=0\) và \(m-3=0\) thì phương trình nghiệm đúng \(\forall x\)
Khi đó \(m=-\frac{1}{2}\) và \(m=3\) (vô lí)
+) Nếu \(2m+1=0\) và \(m-3\ne0\) thì phương trình vô nghiệm
Khi đó:\(m=-\frac{1}{2}\) và \(m\ne3\) (chọn) +) Nếu \(2m+1\ne0\) và \(m-3\ne0\) thì phương trình có nghiệm duy nhất \(x=\frac{m-3}{2m+1}\) Khi đó \(m\ne3\) và \(m\ne-\frac{1}{2}\)
24 tháng 1 2022
1. \(x+3m>3+mx.\Leftrightarrow x+3m-3-mx>0.\\ \Leftrightarrow\left(1-m\right)x+3m-3>0.\\ \Leftrightarrow\left(1-m\right)x>-3m+3.\left(1\right)\)
+) Nếu \(1-m=0.\Leftrightarrow m=1.\) Thay vào (1):
\(0x>-3.1+3.\Leftrightarrow0x>0\) (vô lý).
\(\Rightarrow\) Bất phương trình vô nghiệm.
+) Nếu \(1-m>0.\Leftrightarrow m< 1.\)
Khi đó (1) có nghiệm: \(x>\dfrac{-3m+3}{1-m}.\Leftrightarrow x>\dfrac{-3\left(m-1\right)}{-\left(m-1\right)}.\Leftrightarrow x>3.\)
+) Nếu \(1-m< 0.\Leftrightarrow m>1.\)
Khi đó (1) có nghiệm: \(x< \dfrac{-3m+3}{1-m}.\Leftrightarrow x< 3.\)
DT
24 tháng 1 2022
1/ x=3 , m=1
bl : tìm nghiệm , tạo khoảng thử nghiệm
2/ \(m=\pm\sqrt{-\dfrac{25-2x}{25-x}}\)
\(x=\dfrac{25\left(1+m^2\right)}{2+m^2}\)
3/ x=-m+1
m = \(\left\{{}\begin{matrix}3\\-x+1\end{matrix}\right.\)
4/ m= \(\left\{{}\begin{matrix}x-3\\3\end{matrix}\right.\)
x= m+3
NH
2
21 tháng 11 2021
\(PT\Leftrightarrow\left(m+1\right)x-3x=2m-1\\ \Leftrightarrow x\left(m-2\right)=2m-1\\ \Leftrightarrow x=\dfrac{2m-1}{m-2}\left(m\ne2\right)\)
3 tháng 8 2016
+/ neu a khác 0 thi phuong trình có một nghiệm duy nhất x=-b/a
+/ nếu a=0 va b khác 0 thi phương trình vô nghiệm
a=0 va b=0 thi phuong trình có vô sô nghiệm
VD: giai và biẹn luận phuong trình m^2(x-1)+m=x(3m-2) (1) (với m la tham số và x là ẩn)
ta có phuong trinh(1) <=> m^2x-m^2+m-3mx+2x=0
<=> x(m^2-3m+2)-m^2+m=0 (2)
Nếu m^2-3m+2 khác 0 <=> m khác 2 và m khác 1=> phuong trình co nghiệm duy nhất
x=m-m^2/m^2-3m+2 <=> x=m/m-2
Nếu m^2-3m+2=0 <=> m=2 hoăcm=1
vói m=2 thi phuong trình (2) trở thành 0x-2=0 => phương trình dã cho vô nghiệm
với m=1 thi phwơng trình (2) trở thành 0x =0 => phương trình da cho có vô số nghiệm
PT
1
CM
18 tháng 1 2019
m x - m 2 > 2 x - 4 ⇔ (m - 2)x > (m - 2)(m + 2)
Nếu m > 2 thì m – 2 > 0, bất phương trình có nghiệm là x > m + 2;
Nếu m < 2 thì m – 2 < 0, bất phương trình có nghiệm là x < m + 2;
Nếu m = 2 thì bất phương trình trở thành 0x > 0, bất phương trình vô nghiệm.
13 tháng 2 2022
a: \(\Leftrightarrow mx-m^2+3m=mx-2m+6\)
\(\Leftrightarrow-m^2+5m-6=0\)
\(\Leftrightarrow\left(m-2\right)\left(m-3\right)=0\)
=>m=2 hoặc ,=3
b: Để phương trình là phương trình bậc hai một ẩn thì m+1<>0
hay m<>-1
\(\text{Δ}=\left(2m-2\right)^2-4\left(m+1\right)\left(m-2\right)\)
\(=4m^2-8m+4-4\left(m^2-m-2\right)\)
\(=4m^2-8m+4-4m^2+4m+8\)
=-4m+12
Để phương trình có hai nghiệm phân biệt thì -4m+12>0
=>-4m>-12
hay m<3
Để phương trình có nghiệm kép thì -4m+12=0
hay m=3
Để phương trình vô nghiệm thì -4m+12<0
hay m>3