Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 3x^2-4x+1=0
a=3; b=-4; c=1
Vì a+b+c=0 nên phương trình có hai nghiệm là:
x1=1 và x2=c/a=1/3
b: -x^2+6x-5=0
=>x^2-6x+5=0
a=1; b=-6; c=5
Vì a+b+c=0 nên phương trình có hai nghiệm là;
x1=1; x2=5/1=5

\(1,\Delta=\left(-11\right)^2-4\cdot30=1\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11-1}{2}=5\\x=\dfrac{11+1}{2}=6\end{matrix}\right.\\ 2,\Delta=\left(-1\right)^2-4\left(-20\right)=81\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1-\sqrt{81}}{2}=-4\\x=\dfrac{1+\sqrt{81}}{2}=5\end{matrix}\right.\\ 3,\Delta=14^2-4\cdot24=100\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-14-\sqrt{100}}{2}=-12\\x=\dfrac{-14+\sqrt{100}}{2}=-2\end{matrix}\right.\\ 4,\Delta=8^2-4\left(-2\right)3=88\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-8-\sqrt{88}}{6}=\dfrac{-4+\sqrt{22}}{3}\\x=\dfrac{-8+\sqrt{88}}{6}=\dfrac{-4-\sqrt{22}}{3}\end{matrix}\right.\)

1) \(4x^2-9=0\)
Theo pt ta có: \(a=4;b=0;c=-9\)
\(\Delta=b^2-4ac=0^2-4.4.\left(-9\right)=144>0\)
=> Pt có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{144}}{2.4}=-\dfrac{3}{2}\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{144}}{2.4}=\dfrac{3}{2}\)
2) \(-2x^2+50=0\)
Theo pt ta có: \(a=-2;b=0;c=50\)
\(\Delta b^2-4ac=0^2-4.\left(-2\right).50=400>0\)
=> PT có 2 nghiệm phân biệt
\(x_1=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-0-\sqrt{400}}{2.\left(-2\right)}=5\\ x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-0+\sqrt{400}}{2a}=-5\)
3) \(3x^2+11=0\)
Theo pt ta có: \(a=3;b=0;c=11\)
\(\Delta=b^2-4ac=0^2-4.3.11=-132< 0\)
=> PT vô nghiệm

a: Khi m=9 thì phương trình trở thành:
\(2x^2-19x+39=0\)
\(\Leftrightarrow2x^2-6x-13x+39=0\)
=>(x-3)(2x-13)=0
=>x=13/2 hoặc x=3
b: \(\text{Δ}=\left(2m+1\right)^2-4\cdot2\cdot\left(m^2-9m+39\right)\)
\(=4m^2+4m+1-8m^2+72m-312\)
\(=-4m^2+76m-311\)
\(=-\left(4m^2-76m+361-50\right)\)
\(=-\left(2m-19\right)^2+50\)
Để phương trình có hai nghiệm thì \(-\left(2m-19\right)^2+50>=0\)
\(\Leftrightarrow-\left(2m-19\right)^2>=-50\)
\(\Leftrightarrow\left(2m-19\right)^2< =50\)
hay \(\dfrac{-5\sqrt{2}+19}{2}< =m< =\dfrac{5\sqrt{2}+19}{2}\)
Theo Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2m+1}{2}\\x_1x_2=\dfrac{m^2-9m+39}{2}\end{matrix}\right.\)
Đến đây bạn chỉ cần kết hợp cái x1+x2 và x1=2x2 để lập hệ phương trình, xong sau đó bạn chỉ cần thay vào cái tích rồi tìm m là xong

BÀI 1. Giải các phương trình sau bằng công thức nghiệm hoặc (công thức nghiện thu gọn).
1) x2 - 11x + 38 = 0 ;
2) 6x2 + 71x + 175 = 0 ;
3) 5x2 - 6x + 27 =0 ;
4) - 30x2 + 30x - 7,5 = 0 ;
5) 4x2 - 16x + 17 = 0 ;
6) x2 + 4x - 12 = 0 ;

a: =>(x-7)(x+3)=0
hay \(x\in\left\{7;-3\right\}\)
b: =>2x+7=0
hay x=-7/2
c: \(\Delta=50-4\cdot6\cdot2=50-48=2\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5\sqrt{2}-\sqrt{2}}{12}=\dfrac{\sqrt{2}}{3}\\x_2=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)

7x2 - 6√2x + 2 = 0
a = 7; b' = -3√2; c = 2
Δ' =(b')2 - ac = (-3√2)2 - 7.2 = 4 ⇒ √(Δ') = 2
Phương trình có 2 nghiệm:
x1 = (3√2 + 2)/7; x2 = (3√2 - 2)/7

Phương trình 5 x 2 – 6x -1 = 0 có hệ số a = 5, b’ = -3, c = -1
Ta có: ∆ ’ = b ' 2 – ac = - 3 2 -5.(-1) = 9 + 5 = 14 > 0
∆ ' = 14
Phương trình có hai nghiệm phân biệt :
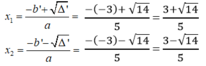
a: \(\Delta=2^2-4\cdot1\cdot\left(-30\right)=124\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-2-2\sqrt{31}}{2}=-1-\sqrt{31}\\x_2=-1+\sqrt{31}\end{matrix}\right.\)
b: \(2x^2-3x-5=0\)
\(\Leftrightarrow2x^2-5x+2x-5=0\)
=>(2x-5)(x+1)=0
=>x=5/2 hoặc x=-1
a.\(x^2+2x-30=0\)
\(\Delta=2^2-4.\left(-30\right)=4+120=124>0\)
=> pt có 2 nghiệm
\(\left\{{}\begin{matrix}x=\dfrac{-2+\sqrt{124}}{2}=\dfrac{-2+2\sqrt{31}}{2}=-1+\sqrt{31}\\x=\dfrac{-2-\sqrt{124}}{2}=-1-\sqrt{31}\end{matrix}\right.\)
b.\(2x^2-3x-5=0\)
Ta có: a-b+c=0
\(\Rightarrow\left\{{}\begin{matrix}x=-1\\x=\dfrac{5}{2}\end{matrix}\right.\)( vi-ét )