Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5,\(hpt\Leftrightarrow\left\{{}\begin{matrix}x\left(x+y\right)\left(x+2\right)=0\\2\sqrt{x^2-2y-1}+\sqrt[3]{y^3-14}=x-2\end{matrix}\right.\)
Thay từng TH rồi làm nha bạn
3,\(hpt\Leftrightarrow\left\{{}\begin{matrix}x-y=\frac{1}{x}-\frac{1}{y}=\frac{y-x}{xy}\\2y=x^3+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(1+\frac{1}{xy}\right)=0\\2y=x^3+1\end{matrix}\right.\)
thay nhá
Bài 1:ĐKXĐ: \(2x\ge y;4\ge5x;2x-y+9\ge0\)\(\Rightarrow2x\ge y;x\le\frac{4}{5}\Rightarrow y\le\frac{8}{5}\)
PT(1) \(\Leftrightarrow\left(x-y-1\right)\left(2x-y+3\right)=0\)
+) Với y = x - 1 thay vào pt (2):
\(\frac{2}{3+\sqrt{x+1}}+\frac{2}{3+\sqrt{4-5x}}=\frac{9}{x+10}\) (ĐK: \(-1\le x\le\frac{4}{5}\))
Anh quy đồng lên đê, chắc cần vài con trâu đó:))
+) Với y = 2x + 3...

a)\(\left\{{}\begin{matrix}2x-3y=1\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot\left(3-2y\right)-3y=1\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6-7y=1\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{7}\\x=3-2\cdot\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{5}{7}\\x=\dfrac{11}{7}\end{matrix}\right.\)b) Biểu diễn lại một biến theo một biến như pt trên rồi giải, ta có :
\(\left\{{}\begin{matrix}2x+4y=5\\4x-2y=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{9}{10}\\y=\dfrac{4}{5}\end{matrix}\right.\)
c) Cách làm tương tự như pt a ta có :
\(\left\{{}\begin{matrix}\dfrac{2}{3}x+\dfrac{1}{2}y=\dfrac{2}{3}\\\dfrac{1}{3}x-\dfrac{3}{4}y=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{9}{8}\\y=-\dfrac{1}{6}\end{matrix}\right.\)
d) Tương tự ta có :
\(\left\{{}\begin{matrix}0,3x-0,2y=0,5\\0,5x+0,4y=1,2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y}=5\\\dfrac{1}{x}-\dfrac{4}{y}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{3}{y}=5\\\dfrac{2}{x}-\dfrac{8}{y}=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y}=11\\\dfrac{1}{x}-\dfrac{4}{y}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\\dfrac{1}{x}=-3+\dfrac{4}{y}=-3+4=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{12}{x-3}-\dfrac{5}{y+2}=63\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{36}{x-3}-\dfrac{15}{y+2}=189\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{44}{x-3}=176\\\dfrac{8}{x-3}+\dfrac{15}{y+2}=-13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3=\dfrac{1}{4}\\\dfrac{15}{y+2}=-13-\dfrac{8}{x-3}=-13-32=-45\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{13}{4}\\y=-\dfrac{1}{3}-2=-\dfrac{7}{3}\end{matrix}\right.\)

Ta có:
Xét \(x=0;y=0\) không là nghiệm của hệ phương trình
Xét \(x\ne0;y\ne0\), ta có:\(\left\{{}\begin{matrix}y\left(x^2+1\right)=2x\left(y^2+1\right)\\\left(x^2+y^2\right)\left(1+\dfrac{1}{x^2y^2}\right)=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x^2+1}{x}=2.\dfrac{y^2+1}{y}\\x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}=2\left(y+\dfrac{1}{y}\right)\\\left(x+\dfrac{1}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2=20\end{matrix}\right.\)
Đặt \(a=x+\dfrac{1}{x};b=y+\dfrac{1}{y}\)
Ta có: \(\left\{{}\begin{matrix}a=2b\\a^2+b^2=20\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=2b\\5b^2=20\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)hoặc\(\left\{{}\begin{matrix}a=-4\\b=-2\end{matrix}\right.\)
*\(\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}=4\\y+\dfrac{1}{y}=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x^2-4x+1=0\\y^2-2y+1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=2-\sqrt{3}\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=2+\sqrt{3}\\y=1\end{matrix}\right.\end{matrix}\right.\)
*\(\left\{{}\begin{matrix}a=-4\\b=-2\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}=-4\\y+\dfrac{1}{y}=-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x^2+4x+1=0\\y^2+2y+1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-2+\sqrt{3}\\y=-1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2-\sqrt{3}\\y=-1\end{matrix}\right.\end{matrix}\right.\)
Vậy tập nghiệm của hệ phương trình là \(\left(2-\sqrt{3};1\right),\left(2+\sqrt{3};1\right),\left(-2+\sqrt{3};-1\right),\left(-2-\sqrt{3};-1\right)\)

1)Điều kiện: \(x + y > 0\)\((1) \Leftrightarrow (x + y)^2 - 2xy + \dfrac{2xy}{x + y} - 1 = 0 \\ \Leftrightarrow (x + y)^3 - 2xy(x + y) + 2xy -(x + y) = 0 \\ \Leftrightarrow (x+y)[(x+y)^2- 1]-2xy(x+y-1)=0 \\ \Leftrightarrow (x+y)(x+y+1)(x+y-1)-2xy(x+y-1)=0 \\ \Leftrightarrow (x + y - 1)[(x+y)(x + y + 1)-2xy] = 0 \\ \Leftrightarrow \left[ \begin{matrix}x + y = 1 \,\, (3) \\ x^2+y^2+x+y=0 \,\, (4) \end{matrix} \right.\)(4) vô nghiệm vì x + y > 0
Thế (3) vào (2) , giải được nghiệm của hệ :\((x =1 ; y = 0)\)và \((x = -2 ; y = 3)\)
\((1)\Leftrightarrow (x-2y)+(2x^3-4x^2y)+(xy^2-2y^3)=0\)\(\Leftrightarrow (x-2y)(1+2x^2+y^2)=0\)
\(\Leftrightarrow x=2y\)(vì \(1+2x^2+y^2>0, \forall x,y\))
Thay vào phương trình (2) giải dễ dàng.

1. \(\left\{{}\begin{matrix}x+y+\dfrac{1}{x}+\dfrac{1}{y}=5\\x^2+y^2+\dfrac{1}{x^2}+\dfrac{1}{y^2}=9\end{matrix}\right.\) ĐKXĐ : \(\left\{{}\begin{matrix}x>0\\y>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2y+xy^2+x+y=5xy\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^4y^2+x^2y^4+x^2+y^2=25x^2y^2\\x^4y^2+x^2y^4+x^2+y^2=9x^2y^2\end{matrix}\right.\)\(\Leftrightarrow0=16x^2y^2\)
\(\Rightarrow\) phương trình vô nghiệm

a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
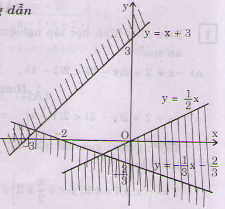
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).
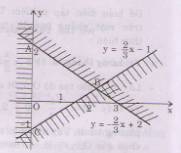

\(\left\{{}\begin{matrix}x^2y+2=y^2\\xy^2+2=x^2\end{matrix}\right.\)
☘ Trừ vế theo vế
\(\Rightarrow x^2y-xy^2=y^2-x^2\)
\(\Leftrightarrow xy\left(x-y\right)+\left(x-y\right)\left(x+y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y+xy\right)=0\)
☘ Trường hợp 1: \(x=y\)
☘ Trường hợp 2: \(x+y+xy=0\)
\(\Leftrightarrow y\left(1+x\right)=-x\)
\(\Leftrightarrow y=-\dfrac{x}{1+x}\) thay vào phương trình thứ 2
\(\Rightarrow x\left(-\dfrac{x}{1+x}\right)^2+2=x^2\)
\(\Leftrightarrow x^3+2\left(1+x\right)^2-x^2\left(1+x\right)^2=0\)
\(\Leftrightarrow x^4+x^3-x^2-4x-2=0\)
\(\Leftrightarrow\left(x^2+2x+2\right)\left(x^2-x-1\right)=0\)
⚠ Tự giải tiếp nha. Mà chưa học hệ phương trình đối xưng gì đó nên không chắc đâu.
Lấy pt (1)-pt(2) ta có:
\(x^2y-xy^2=y^2-x^2\)
<=>\(xy(x-y)+(x-y)(x+y)=0\)
<=>\((x-y)(x+y+xy)=0\)
=>x=y hoặc x+y+xy=0=>y(x+1)=-x=>y=\(\frac{-x}{x+1} \)
Với x=y
=>\(x^3-x^2+2=0\)
=>x=-1
=>y=-1
Với y=\(\frac{-x}{x+1} \)
=>\(\frac{-x^3}{x+1} +2-\frac{x^2}{(x+1)^2}=0 \)
tự giải nốt nha
Lời giải:
HPT tương đương:
\(\left\{\begin{matrix} 2x^2y=y^2+1\\ 2xy^2=x^2+1\end{matrix}\right.\)
Trừ hai pt cho nhau thì:
$2xy(x-y)+x^2-y^2=0$
$\Leftrightarrow 2xy(x-y)+(x-y)(x+y)=0$
$\Leftrightarrow (x-y)(2xy+x+y)=0$
$\Leftrightarrow x-y=0$ hoặc $2xy+x+y=0$
Nếu $x-y=0\Leftrightarrow x=y$. Thay vào pt (1):
$2x^2=x+\frac{1}{x}$
$\Rightarrow 2x^3=x^2+1$
$\Leftrightarrow (x-1)(2x^2+x+1)=0$
Đến đấy thì đơn giản rồi.
Nếu $2xy+x+y=0$:
Từ $2x^2=y+\frac{1}{y}=\frac{y^2+1}{y}$
Mà $2x^2>0; y^2+1>0$ với mọi $x,y\neq 0$ nên $y>0$
Tương tự $x>0$
$\Rightarrow 2xy+x+y>0$. Do đó TH này loại
Vậy...........