TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
15 tháng 9 2021
a, ĐK: \(x\ge11\)
\(\sqrt{x+\sqrt{x-11}}+\sqrt{x-\sqrt{x-11}}=4\)
\(\Leftrightarrow x+\sqrt{x-11}+x-\sqrt{x-11}+2\sqrt{x^2-x+11}=16\)
\(\Leftrightarrow2x+2\sqrt{x^2-x+11}=16\)
\(\Leftrightarrow x+\sqrt{x^2-x+11}=8\)
Ta thấy \(x+\sqrt{x^2-x+11}>11>\text{}8\)
\(\Rightarrow\) phương trình vô nghiệm.
15 tháng 9 2021
\(a,\sqrt{x+\sqrt{x-11}}+\sqrt{x-\sqrt{x-11}}=4\left(x\ge11\right)\\ \Leftrightarrow x+\sqrt{x-11}+x-\sqrt{x-11}+2\sqrt{\left(x+\sqrt{x-11}\right)\left(x-\sqrt{x-11}\right)}=16\\ \Leftrightarrow2x+2\sqrt{x^2-x+11}=16\\ \Leftrightarrow x+\sqrt{x^2-x+11}=8\\ \Leftrightarrow\sqrt{x^2-x+11}=8-x\\ \Leftrightarrow x^2-x+11=x^2-16x+64\\ \Leftrightarrow15x=53\\ \Leftrightarrow x=\dfrac{53}{15}\left(ktm\right)\)
\(b,\sqrt{x+2+3\sqrt{2x-5}}+\sqrt{x-2-\sqrt{2x-5}}=2\sqrt{2}\left(x\ge\dfrac{5}{2}\right)\\ \Leftrightarrow\sqrt{2x-5+6\sqrt{2x-5}+9}+\sqrt{2x-5-2\sqrt{2x-5}+1}=4\\ \Leftrightarrow\sqrt{\left(\sqrt{2x-5}+3\right)^2}+\sqrt{\left(\sqrt{2x-5}-1\right)^2}=4\\ \Leftrightarrow\sqrt{2x-5}+3+\left|\sqrt{2x-5}-1\right|=4\\ \Leftrightarrow\left|\sqrt{2x-5}-1\right|=1-\sqrt{2x-5}\\ \Leftrightarrow\sqrt{2x-5}-1\le0\\ \Leftrightarrow\sqrt{2x-5}\le1\\ \Leftrightarrow2x-5\le1\Leftrightarrow x\le\dfrac{5}{2}\\ \Leftrightarrow x=\dfrac{5}{2}\)
13 tháng 10 2021
\(ĐK:-3\le x\le\dfrac{3}{2}\\ PT\Leftrightarrow11-x-4\sqrt{x+3}-2\sqrt{3-2x}=0\\ \Leftrightarrow\left(x+3-4\sqrt{x+3}+4\right)+\left(3-2x-2\sqrt{3-2x}+1\right)=0\\ \Leftrightarrow\left(\sqrt{x+3}-2\right)^2+\left(\sqrt{3-2x}-1\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x+3}=2\\\sqrt{3-2x}=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+3=2\\3-2x=1\end{matrix}\right.\Leftrightarrow x=1\left(tm\right)\)
TN
0
OK
2
18 tháng 5 2021
x=\(\frac{1}{392}\)(729-28\(\sqrt{2}\)+\(\sqrt{1457-56\sqrt{2}}\)
31 tháng 12 2023
a: \(\sqrt{x^2+6x+9}=\sqrt{11+6\sqrt{2}}\)
=>\(\sqrt{\left(x+3\right)^2}=\sqrt{\left(3+\sqrt{2}\right)^2}\)
=>\(\left|x+3\right|=\left|3+\sqrt{2}\right|=3+\sqrt{2}\)
=>\(\left[{}\begin{matrix}x+3=3+\sqrt{2}\\x+3=-3-\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-6-\sqrt{2}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}2x-y=4\\x+2y=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x-2y=8\\x+2y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-2y+x+2y=8-3\\2x-y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\cdot1-4=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
NT
0
HA
3
VT
4 tháng 10 2019
điều kiện x+3>=0 và 3-2x<=0 hay -3\(\le x\le\frac{3}{2}\) (1)
\(\sqrt{x+3}=a\);\(\sqrt{3-2x}=b\) => x=\(a^2-3\) và 2a2+b2=3
thay vào ta được x+4a+2b=11 <=>a2-3+4a+2b=11 <=>a2+4a+2b=14
ta có hệ phương trình \(\hept{\begin{cases}2a^2+b^2=9\\a^2+4a+2b=14\end{cases}}\)<=>\(\hept{\begin{cases}2a^2+b^2-a^2-4a-2b=3-14\\2a^2+b^2=9\end{cases}}\)<=>\(\hept{\begin{cases}\left(a-2\right)^2+\left(b-1\right)^2=0\\2a^2+b^2=9\end{cases}}\)<=>\(\hept{\begin{cases}a=2\\b=1\end{cases}}\)<=>\(\hept{\begin{cases}\sqrt{x+3}=2\\\sqrt{3-2x}=1\end{cases}}\)<=>x=1 (thỏa mãn điều kiện (1))
vậy pt có nghiệm duy nhất x=1
N
4 tháng 10 2019
\(DK:x\in\left[-3;\frac{3}{2}\right]\)
PT\(\Leftrightarrow\left(x-1\right)+\left(4\sqrt{x+3}-8\right)+\left(2\sqrt{3-2x}-2\right)=0\)
\(\Leftrightarrow\left(x-1\right)+\frac{4\left(x-1\right)}{\sqrt{x+3}+2}-\frac{4\left(x-1\right)}{\sqrt{3-2x}+1}=0\)
\(\Leftrightarrow\left(x-1\right)\left(1+\frac{4}{\sqrt{x+3}+2}-\frac{4}{\sqrt{3-2x}+1}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\left(1\right)\\1+\frac{4}{\sqrt{x+3}+2}-\frac{4}{\sqrt{3-2x}+1}=0\left(2\right)\end{cases}}\)
PT(2) khac khong voi moi \(x\in\left[-3;\frac{3}{2}\right]\)
Vay nghiem cua PT la \(x=1\)
1 tháng 10 2021
Tham khảo:
1) Giải phương trình : \(11\sqrt{5-x}+8\sqrt{2x-1}=24+3\sqrt{\left(5-x\right)\left(2x-1\right)}\) - Hoc24
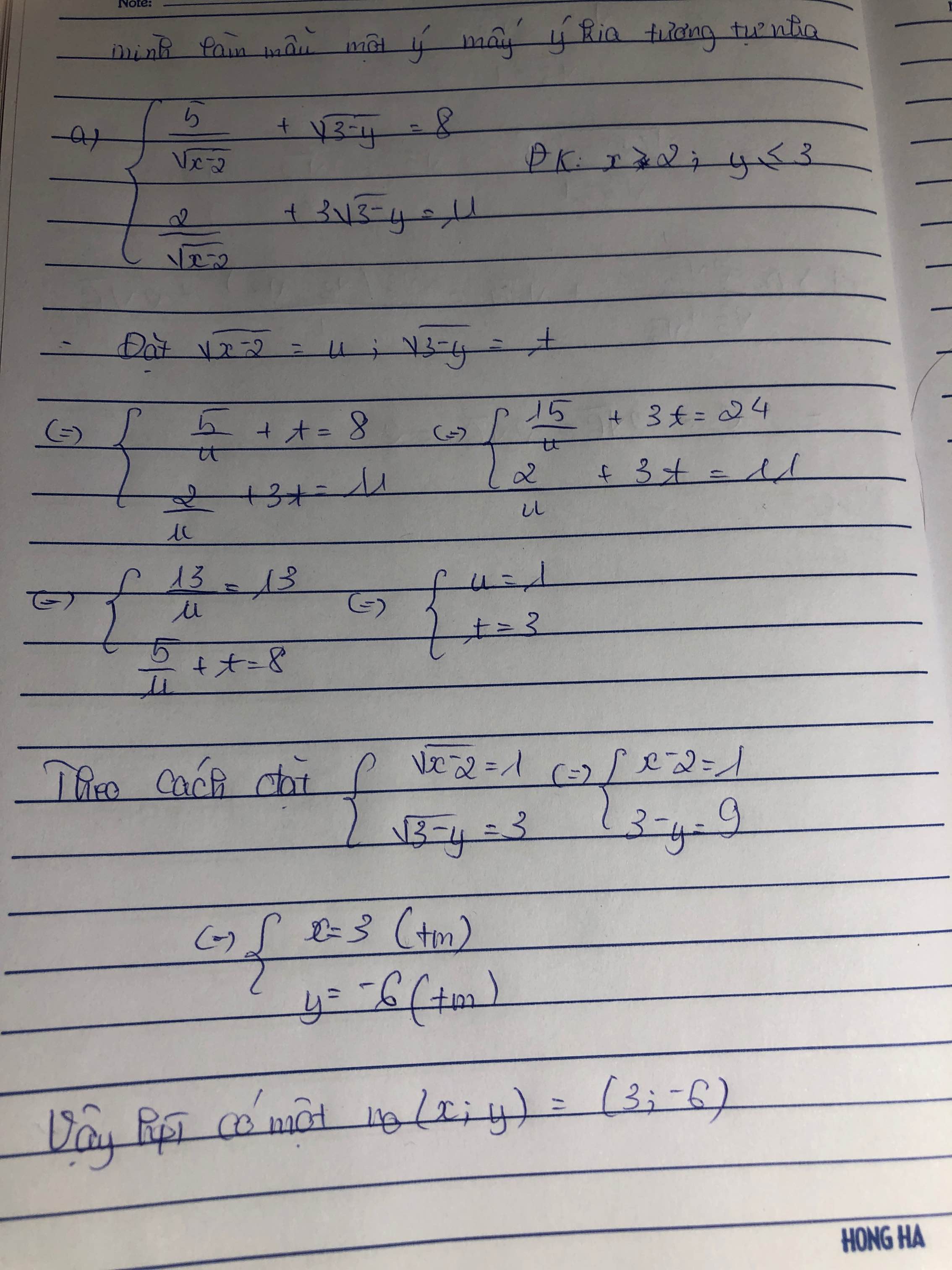
ĐKXĐ: \(\left\{{}\begin{matrix}x+3\ge0\\3-2x\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-3\\x\le\dfrac{3}{2}\end{matrix}\right.\)
PT\(\Leftrightarrow x-1+4\left(\sqrt{x+3}-2\right)+2\left(\sqrt{3-2x}-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)+4.\dfrac{x+3-4}{\sqrt{x+3}+2}+2.\dfrac{3-2x-1}{\sqrt{3-2x}+1}=0\)
\(\Leftrightarrow\left(x-1\right)+4.\dfrac{x-1}{\sqrt{x+3}+2}-2.\dfrac{2\left(x-1\right)}{\sqrt{3-2x}+1}=0\)
\(\Leftrightarrow\left(x-1\right)\left[1+\dfrac{4}{\sqrt{x+3}+2}-\dfrac{4}{\sqrt{3-2x}+1}\right]=0\)
TH1:\(x-1=0\Leftrightarrow x=1\left(tmđk\right)\)
TH2:\(1+\dfrac{4}{\sqrt{x+3}+2}-\dfrac{4}{\sqrt{3-2x}+1}=0\)(VN)