CV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 10 2021
d) \(x^2+y^2-4x+4y=1\\ \Rightarrow\left(x-2\right)^2+\left(y+2\right)^2=8\)
\(\Rightarrow8=\left(x-2\right)^2+\left(y+2\right)^2\ge\left(x-2\right)^2\)
\(\Rightarrow\left(x-2\right)^2\le8\)
Mà \(\left(x-2\right)^2\) là SCP và là số chẵn nên \(\left(x-2\right)^2\in\left\{0;4\right\}\)
Th1: \(\left(x-2\right)^2=0\Rightarrow\left(y+2\right)^2=8\left(vôlí\right)\)
Th2: \(\left(x-2\right)^2=4\Rightarrow\left(y+2\right)^2=4\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2=-2\\y+2=-2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=-2\\y+2=2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=2\\y+2=-2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=2\\y+2=2\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=0\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-4\right);\left(0;0\right);\left(4;-4\right);\left(4;0\right)\right\}\)
LD
2
KN
24 tháng 8 2020
x4 - 2y2 = 1 => x4 - 1 = 2y2 ( 1 )
Dễ thấy : x lẻ \(x^4\equiv1\) ( mod 4 )
=> y2 chẵn => y chẵn
Đặt \(x=2k+1;y=2n\left(k;n\in Z\right)\). Ta có :
\(\left(4k^2+4k+1\right)^2-1=8n^2\)
\(\Leftrightarrow\left(4k^2+4k+2\right)\left(4k^2+4k\right)=8n^2\)
\(\Leftrightarrow\left(2k^2+2k+1\right)\left(k^2+k\right)=n^2\)
Với k = 0 thì \(y=0\) ( tm )
Thay y = 0 vào ( 1 ) ta được \(x=\pm1\) ( tm )
Với \(k\ge1\)
Đặt \(k^2+k=m\)
\(\Rightarrow\left(2m+1\right)m=n^2\)
=> m ; 2m + 1 là SCP
Ta lại có : \(k^2< k^2+k< \left(k+1\right)^2\)
Vì k2 + k kẹp giữa 2 SCP liên tiếp nên k2 + k không thể là SCP
Vậy pt có các nghiệm ( x ; y ) là : ( 1 ; 0 ) ; ( - 1 ; 0 )
24 tháng 8 2020
Tohru ( ʚ๖ۣۜTεαм ๖ۣۜFℓαʂɦɞ ) làm vậy có dài không bạn?
\(x^4-2y^2=1\Leftrightarrow x^4=1+2y^2\)
Do \(\hept{\begin{cases}x^4\ge0\forall x\\2y^2\ge0\forall y\end{cases}}\)
Để x,y nguyên => \(\hept{\begin{cases}x^4=1\\2y^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\pm1\\y=0\end{cases}}}\)
5 tháng 10 2021
a, TK: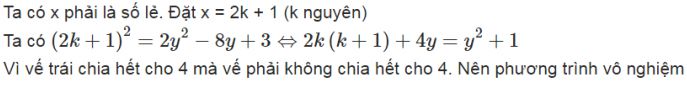
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
NT
0
PA
2
HP
3 tháng 10 2021
a. 3x2 - 4y2 = 18
<=> \(\left\{{}\begin{matrix}3x^2=18+4y^2\\4y^2=-\left(3x^2-18\right)\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{18+4y^2}{3}}\\y=\sqrt{\dfrac{-3x^2+18}{4}}\end{matrix}\right.\)
b, c, d tương tự nhé
HP
3 tháng 10 2021
b. 19x2 + 28y2 = 2001
<=> \(\left\{{}\begin{matrix}19x^2=2001-28y^2\\28y^2=2001-19x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{2001-28y^2}{19}}\\y=\sqrt{\dfrac{2001-19x^2}{28}}\end{matrix}\right.\)
c. x2 = 2y2 - 8y + 3
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\8y=2y^2+3-x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\y=\dfrac{2y^2+3-x^2}{8}\end{matrix}\right.\)
d. x2 + y2 - 4x + 4y = 1
<=> \(\left\{{}\begin{matrix}x^2=1-y^2+4x-4y\\y^2=1-x^2+4x-4y\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{1-y^2+4x-4y}\\y=\sqrt{1-x^2+4x-4y}\end{matrix}\right.\)
TH
0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2023
\(x^2+2z+y^2-2x+z^2-2y+3=0\)
\(\Leftrightarrow\left(x^2-2x+1\right)+\left(y^2-2y+1\right)+\left(z^2-2z+1\right)=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=0\)
Do \(\left\{{}\begin{matrix}\left(x-1\right)^2\ge0\\\left(y-1\right)^2\ge0\\\left(z-1\right)^2\ge0\end{matrix}\right.\) ;\(\forall x;y;z\)
\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2+\left(z-1\right)^2\ge0\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}x-1=0\\y-1=0\\z-1=0\end{matrix}\right.\) \(\Rightarrow x=y=z=1\)
Ngu quá có thế cũng không làm được