Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(3x-2\sqrt{x-1}=4\) (ĐK: x ≥ 1)
\(\Rightarrow3x-2\sqrt{x-1}-4=0\)
\(\Rightarrow3x-6-2\sqrt{x-1}+2=0\)
\(\Rightarrow3\left(x-2\right)-2\left(\sqrt{x-1}-1\right)=0\)
\(\Rightarrow3\left(x-2\right)-2.\dfrac{x-2}{\sqrt{x-1}+1}=0\)
\(\Rightarrow\left(x-2\right)\left[3-\dfrac{2}{\sqrt{x-1}+1}\right]=0\)
*TH1: x = 2 (t/m)
*TH2: \(3-\dfrac{2}{\sqrt{x-1}+1}=0\)
\(\Rightarrow3=\dfrac{2}{\sqrt{x-1}+1}\)
\(\Rightarrow3\sqrt{x-1}+3=2\)
\(\Rightarrow3\sqrt{x-1}=-1\) (vô lí)
Vậy S = {2}
b) \(\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\) (ĐK: \(-\dfrac{1}{4}\le x\le3\) )
\(\Rightarrow\sqrt{4x+1}-3-\sqrt{x+2}+2-\sqrt{3-x}+1=0\)
\(\Rightarrow\dfrac{4x-8}{\sqrt{4x+1}+3}-\dfrac{x-2}{\sqrt{x+2}+2}+\dfrac{x-2}{\sqrt{3-x}+1}=0\)
\(\Rightarrow\left(x-2\right)\left(\dfrac{4}{\sqrt{4x+1}+3}-\dfrac{1}{\sqrt{x+2}+2}+\dfrac{1}{\sqrt{3-x}+1}\right)=0\)
=> x = 2
\(a,3x-2\sqrt{x-1}=4\left(x\ge1\right)\\ \Leftrightarrow-2\sqrt{x-1}=4-3x\\ \Leftrightarrow4\left(x-1\right)=16-24x+9x^2\\ \Leftrightarrow9x^2-28x+20=0\\ \Leftrightarrow\left(x-2\right)\left(9x-10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=\dfrac{10}{9}\left(tm\right)\end{matrix}\right.\)
\(b,\sqrt{4x+1}-\sqrt{x+2}=\sqrt{3-x}\left(-\dfrac{1}{4}\le x\le3\right)\\ \Leftrightarrow4x+1+x+2-2\sqrt{\left(4x+1\right)\left(x+2\right)}=3-x\\ \Leftrightarrow-2\sqrt{\left(4x+1\right)\left(x+2\right)}=2-6x\\ \Leftrightarrow\sqrt{4x^2+9x+2}=3x-1\\ \Leftrightarrow4x^2+9x+2=9x^2-6x+1\\ \Leftrightarrow5x^2-15x-1=0\\ \Leftrightarrow\Delta=225+20=245\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{15-\sqrt{245}}{10}=\dfrac{15-7\sqrt{5}}{10}\left(ktm\right)\\x=\dfrac{15+\sqrt{245}}{10}=\dfrac{15+7\sqrt{5}}{10}\left(tm\right)\end{matrix}\right.\Leftrightarrow x=\dfrac{15+7\sqrt{5}}{10}\)

a) \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\) (ĐK: \(x\ge1\))
\(\Leftrightarrow\sqrt{x-1}+\sqrt{4\left(x-1\right)}-\sqrt{25\left(x-1\right)}+2=0\)
\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\)
\(\Leftrightarrow-2\sqrt{x-1}=-2\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{2}{2}\)
\(\Leftrightarrow\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=1\)
\(\Leftrightarrow x=2\left(tm\right)\)
b) \(\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}=16\) (ĐK: \(x\ge-1\))
\(\Leftrightarrow\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}+\sqrt{4\left(x+1\right)}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}=16\)
\(\Leftrightarrow\sqrt{x+1}=4\)
\(\Leftrightarrow x+1=16\)
\(\Leftrightarrow x=15\left(tm\right)\)

c: Ta có: \(\sqrt{x-1}+\sqrt{9x-9}-\sqrt{4x-4}=4\)
\(\Leftrightarrow2\sqrt{x-1}=4\)
\(\Leftrightarrow x-1=4\)
hay x=5
e: Ta có: \(\sqrt{4x^2-28x+49}-5=0\)
\(\Leftrightarrow\left|2x-7\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-7=5\\2x-7=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=1\end{matrix}\right.\)
a. ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow \sqrt{(x-2)^2}=2-x$
$\Leftrightarrow |x-2|=2-x$
$\Leftrightarrow 2-x\geq 0$
$\Leftrightarrow x\leq 2$
b. ĐKXĐ: $x\geq 2$
PT $\Leftrightarrow \sqrt{4}.\sqrt{x-2}-\frac{1}{5}\sqrt{25}.\sqrt{x-2}=3\sqrt{x-2}-1$
$\Leftrightarrow 2\sqrt{x-2}-\sqrt{x-2}=3\sqrt{x-2}-1$
$\Leftrightarrow 1=2\sqrt{x-2}$
$\Leftrightarrow \frac{1}{2}=\sqrt{x-2}$
$\Leftrightarrow \frac{1}{4}=x-2$
$\Leftrightarrow x=\frac{9}{4}$ (tm)

cấy pt dạng ni lớp 8 học rồi mà :v
chỉ là thêm công thức nghiệm vào thôi ._.
1. ( x + 2 )( x + 4 )( x + 6 )( x + 8 ) + 16 = 0
<=> [ ( x + 2 )( x + 8 ) ][ ( x + 4 )( x + 6 ) ] + 16 = 0
<=> ( x2 + 10x + 16 )( x2 + 10x + 24 ) + 16 = 0
Đặt t = x2 + 10x + 16
pt <=> t( t + 8 ) + 16 = 0
<=> t2 + 8t + 16 = 0
<=> ( t + 4 )2 = 0
<=> ( x2 + 10x + 16 + 4 )2 = 0
<=> ( x2 + 10x + 20 )2 = 0
=> x2 + 10x + 20 = 0
Δ' = b'2 - ac = 25 - 20 = 5
Δ' > 0 nên phương trình có hai nghiệm phân biệt
\(x_1=\frac{-b'+\sqrt{\text{Δ}'}}{a}=-5+\sqrt{5}\)
\(x_2=\frac{-b'-\sqrt{\text{Δ}'}}{a}=-5-\sqrt{5}\)
Vậy ...
2. ( x + 1 )( x + 2 )( x + 3 )( x + 4 ) - 24 = 0
<=> [ ( x + 1 )( x + 4 ) ][ ( x + 2 )( x + 3 ) ] - 24 = 0
<=> ( x2 + 5x + 4 )( x2 + 5x + 6 ) - 24 = 0
Đặt t = x2 + 5x + 4
pt <=> t( t + 2 ) - 24 = 0
<=> t2 + 2t - 24 = 0
<=> ( t - 4 )( t + 6 ) = 0
<=> ( x2 + 5x + 4 - 4 )( x2 + 5x + 4 + 6 ) = 0
<=> x( x + 5 )( x2 + 5x + 10 ) = 0
Vì x2 + 5x + 10 có Δ = -15 < 0 nên vô nghiệm
=> x = 0 hoặc x = -5
Vậy ...
3. ( x - 1 )( x - 3 )( x - 5 )( x - 7 ) - 20 = 0
<=> [ ( x - 1 )( x - 7 ) ][ ( x - 3 )( x - 5 ) ] - 20 = 0
<=> ( x2 - 8x + 7 )( x2 - 8x + 15 ) - 20 = 0
Đặt t = x2 - 8x + 7
pt <=> t( t + 8 ) - 20 = 0
<=> t2 + 8t - 20 = 0
<=> ( t - 2 )( t + 10 ) = 0
<=> ( x2 - 8x + 7 - 2 )( x2 - 7x + 8 + 10 ) = 0
<=> ( x2 - 8x + 5 )( x2 - 7x + 18 ) = 0
<=> \(\orbr{\begin{cases}x^2-8x+5=0\\x^2-7x+18=0\end{cases}}\)
+) x2 - 8x + 5 = 0
Δ' = b'2 - ac = 16 - 5 = 11
Δ' > 0 nên có hai nghiệm phân biệt
\(x_1=\frac{-b'+\sqrt{\text{Δ}'}}{a}=-4+\sqrt{11}\)
\(x_2=\frac{-b'+\sqrt{\text{Δ}'}}{a}=-4-\sqrt{11}\)
+) x2 - 7x + 18 = 0
Δ = b2 - 4ac = 49 - 72 = -23 < 0 => vô nghiệm
Vậy ...

a/ \(\left(x-2\right)^2=11+6\sqrt{2}\)
\(\Leftrightarrow\left(x-2\right)^2=\left(3+\sqrt{2}\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3+\sqrt{2}\\x-2=-3-\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5+\sqrt{2}\\x=-1-\sqrt{2}\end{matrix}\right.\)
b/ \(x^2-10x+25=27-10\sqrt{2}\)
\(\Leftrightarrow\left(x-5\right)^2=\left(5-\sqrt{2}\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=5-\sqrt{2}\\x-5=\sqrt{2}-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=10-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
c/ \(4x^2+4x+1=28-10\sqrt{3}\)
\(\Leftrightarrow\left(2x+1\right)^2=\left(5-\sqrt{3}\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=5-\sqrt{3}\\2x+1=\sqrt{3}-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{4-\sqrt{3}}{2}\\x=\frac{-6+\sqrt{3}}{2}\end{matrix}\right.\)
d/ \(x^2+2\sqrt{5}x+5=21-4\sqrt{5}\)
\(\Leftrightarrow\left(x+\sqrt{5}\right)^2=\left(2\sqrt{5}-1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\sqrt{5}=2\sqrt{5}-1\\x+\sqrt{5}=1-2\sqrt{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{5}-1\\x=1-3\sqrt{5}\end{matrix}\right.\)
e/ \(x^2+2\sqrt{12}x+12=13-4\sqrt{3}\)
\(\Leftrightarrow\left(x+2\sqrt{3}\right)^2=\left(2\sqrt{3}-1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2\sqrt{3}=2\sqrt{3}-1\\x+2\sqrt{3}=1-2\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1-4\sqrt{3}\end{matrix}\right.\)
f/ \(4x^2-12\sqrt{2}x+18=51-10\sqrt{2}\)
\(\Leftrightarrow\left(2x-3\sqrt{2}\right)^2=\left(5\sqrt{2}-1\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5\sqrt{2}=5\sqrt{2}-1\\2x-2\sqrt{2}=1-5\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{10\sqrt{2}-1}{2}\\x=\frac{1-3\sqrt{2}}{2}\end{matrix}\right.\)

1) \(\sqrt[]{9\left(x-1\right)}=21\)
\(\Leftrightarrow9\left(x-1\right)=21^2\)
\(\Leftrightarrow9\left(x-1\right)=441\)
\(\Leftrightarrow x-1=49\Leftrightarrow x=50\)
2) \(\sqrt[]{1-x}+\sqrt[]{4-4x}-\dfrac{1}{3}\sqrt[]{16-16x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}+\sqrt[]{4\left(1-x\right)}-\dfrac{1}{3}\sqrt[]{16\left(1-x\right)}+5=0\)
\(\)\(\Leftrightarrow\sqrt[]{1-x}+2\sqrt[]{1-x}-\dfrac{4}{3}\sqrt[]{1-x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}\left(1+3-\dfrac{4}{3}\right)+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}.\dfrac{8}{3}=-5\)
\(\Leftrightarrow\sqrt[]{1-x}=-\dfrac{15}{8}\)
mà \(\sqrt[]{1-x}\ge0\)
\(\Leftrightarrow pt.vô.nghiệm\)
3) \(\sqrt[]{2x}-\sqrt[]{50}=0\)
\(\Leftrightarrow\sqrt[]{2x}=\sqrt[]{50}\)
\(\Leftrightarrow2x=50\Leftrightarrow x=25\)
1) \(\sqrt{9\left(x-1\right)}=21\) (ĐK: \(x\ge1\))
\(\Leftrightarrow3\sqrt{x-1}=21\)
\(\Leftrightarrow\sqrt{x-1}=7\)
\(\Leftrightarrow x-1=49\)
\(\Leftrightarrow x=49+1\)
\(\Leftrightarrow x=50\left(tm\right)\)
2) \(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\) (ĐK: \(x\le1\))
\(\Leftrightarrow\sqrt{1-x}+2\sqrt{1-x}-\dfrac{4}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}=-5\) (vô lý)
Phương trình vô nghiệm
3) \(\sqrt{2x}-\sqrt{50}=0\) (ĐK: \(x\ge0\))
\(\Leftrightarrow\sqrt{2x}=\sqrt{50}\)
\(\Leftrightarrow2x=50\)
\(\Leftrightarrow x=\dfrac{50}{2}\)
\(\Leftrightarrow x=25\left(tm\right)\)
4) \(\sqrt{4x^2+4x+1}=6\)
\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)
\(\Leftrightarrow\left|2x+1\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\left(ĐK:x\ge-\dfrac{1}{2}\right)\\2x+1=-6\left(ĐK:x< -\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
5) \(\sqrt{\left(x-3\right)^2}=3-x\)
\(\Leftrightarrow\left|x-3\right|=3-x\)
\(\Leftrightarrow x-3=3-x\)
\(\Leftrightarrow x+x=3+3\)
\(\Leftrightarrow x=\dfrac{6}{2}\)
\(\Leftrightarrow x=3\)

\(x^4-9x^2+24x-16=\)\(0\)
\(\Leftrightarrow x^4-\left(9x^2-24x+16\right)=0\)
\(\Leftrightarrow x^4-\left(3x-4\right)^2=0\)
\(\Leftrightarrow\left(x^2+3x-4\right)\left(x^2-3x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-1\right)\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]=0\)
Vì \(\left(x-\frac{3}{2}\right)^2+\frac{7}{4}>0\forall x\)nên:
\(\left(x+4\right)\left(x-1\right)=0:\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]\)
\(\Leftrightarrow\left(x+4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)
Vậy phương trình có tập nghiệm \(S=\left\{1;-4\right\}\)
\(x^4=6x^2+12x+\)\(8\)
\(\Leftrightarrow x^4-2x^2+1=4x^2+12x+9\)
\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow|x^2-1|=|2x+3|\)\(|\)
xét các trường hợp:
- Trường hợp 1:
\(x^2-1=2x+3\)
\(\Leftrightarrow x^2-1-2x-3=0\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow\left(x-1\right)^2-5=0\Leftrightarrow\left(x-1\right)^2=5\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=\sqrt{5}\\x-1=-\sqrt{5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{cases}}}\)
-Trường hợp 2:
\(x^2-1=-2x-3\)
\(\Leftrightarrow x^2-1+2x+3=0\)
\(\Leftrightarrow x^2+2x+2=0\)
\(\Leftrightarrow\left(x+1\right)^2+1=0\)
\(\Leftrightarrow\left(x+1\right)^2=-1\left(vn\right)\)(vô nghiệm)
Vậy phương trình có tập nghiệm: \(S=\left\{1\pm\sqrt{5}\right\}\)
a) 9 x 4 − 10 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 9 t 2 − 10 t + 1 = 0 ( 2 )
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t 1 = 1 ; t 2 = c / a = 1 / 9
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1.
Vậy phương trình (1) có tập nghiệm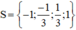
b)
5 x 4 + 2 x 2 - 16 = 10 - x 2 ⇔ 5 x 4 + 2 x 2 - 16 - 10 + x 2 = 0 ⇔ 5 x 4 + 3 x 2 - 26 = 0
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 5 t 2 + 3 t − 26 = 0 ( 2 )
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 3 2 − 4.5 ⋅ ( − 26 ) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
Đối chiếu điều kiện chỉ có t 1 = 2 thỏa mãn
+ Với t = 2 ⇒ ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
c) 0 , 3 x 4 + 1 , 8 x 2 + 1 , 5 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó, (1) trở thành : 0 , 3 t 2 + 1 , 8 t + 1 , 5 = 0 ( 2 )
Giải (2) :
có a = 0,3 ; b = 1,8 ; c = 1,5
⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm t 1 = − 1 và t 2 = − c / a = − 5
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2 x 4 + x 2 = 1 − 4 x 2 ⇔ 2 x 4 + x 2 + 4 x 2 − 1 = 0 ⇔ 2 x 4 + 5 x 2 − 1 = 0 ( 1 )
Đặt t = x 2 , điều kiện t > 0.
Khi đó (1) trở thành : 2 t 2 + 5 t - 1 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 5 2 − 4.2 ⋅ ( − 1 ) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
Đối chiếu với điều kiện thấy có nghiệm t 1 thỏa mãn.
Vậy phương trình có tập nghiệm