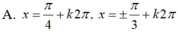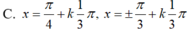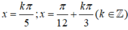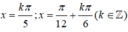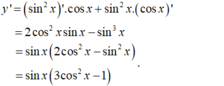Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,Pt \(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x=-\dfrac{\pi}{4}-arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\) ,\(k\in Z\)
b) Pt \(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{4}{5}\Rightarrow sina=\dfrac{3}{5}\)
Pttt:\(cosx.cosa-sina.sinx=\dfrac{3}{5}\)
\(\Leftrightarrow cos\left(x+a\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-a+arc.cos\left(\dfrac{3}{5}\right)+2k\pi\\x=-a-arc.cos\left(\dfrac{3}{5}\right)+2k\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
c) Pt\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}.sin3x=1\)
Đặt \(cosa=\dfrac{3}{5}\Rightarrow sina=\dfrac{4}{5}\)
Pttt:\(cos3x.cosa+sin3a.sina=1\)
\(\Leftrightarrow cos\left(3x-a\right)=1\)
\(\Leftrightarrow x=\dfrac{a}{3}+\dfrac{k2\pi}{3}\)(\(k\in Z\))
Vậy...
1)\(1+2sinx=2cosx\)
\(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left(cosx-sinx\right)^2=\dfrac{1}{4}\)
\(\Leftrightarrow cosx^2+sinx^2-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow1-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow2cosxsinx=\dfrac{3}{4}\)
\(\Leftrightarrow sin2x=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x=arcsin\dfrac{3}{8}+k\pi\\x=\pi-arcsin\dfrac{3}{8}+k\pi\end{matrix}\right.\) \(\left(K\in Z\right)\)
b) \(4cosx-3sinx=3\)
\(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{3}{5},sina=\dfrac{4}{5}\)
Khi đó:
\(sinacosx-cosasinx=\dfrac{3}{5}\)
\(\Leftrightarrow sin\left(a-x\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-x=arcsin\dfrac{3}{5}+k2\pi\\a-x=\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a-arcsin\dfrac{3}{5}+k2\pi\\x=a-\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
3)\(3cos3x+4sin3x=5\)
\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}sin3x=1\)
Đặt \(sina=\dfrac{3}{5},cosa=\dfrac{4}{5}\)
khi đó: \(sinacos3x+cosasin3x=1\)
\(\Leftrightarrow sin\left(a+3x\right)=\dfrac{\pi}{2}\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}-a+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}-\dfrac{1}{3}a+k\dfrac{2}{3}\pi\),\(k\in Z\)
Chúc bạn học tốt^^

Chọn A
Ta có: sin 3 x + 3 cos 3 x – 3 sin x cos 2 x – sin 2 x cos x = 0
Do cosx=0 không là nghiệm của phương trình nên chia hai vế cho cos 3 x ≠ 0 ta được phương trình:


Làm bằng máy tính phải kiểm tra đáp án lần lượt lâu hơn tự luận nhiều
Máy tính casio FX-570VN:
- Chuyển chế độ góc về radian
- Để kiểm tra đáp án A, nhập:
\(\frac{d}{dx}\left(sin\left(3X\right)\right)|_{x=X}-3cos\left(3X\right)\)
Sau đó bấm CALC rồi cho 1 giá trị X bất kì rồi "=". Nếu kết quả bằng 0 thì đó là đáp án đúng
Với các đáp án khác, chỉ cần thay 3cos(3X) bằng đáp án tương ứng là được, ví dụ kiểm tra đáp án C thì nhập
\(\frac{d}{dx}\left(sin\left(3X\right)\right)|_{x=X}--3cos\left(3X\right)\)