Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(ĐK:x\ne-1\\ PT\Leftrightarrow\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x+1\right)\left(x^2+x+1\right)}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{x-1}{x+1}=\dfrac{1}{4}\\ \Leftrightarrow4x-4=x+1\\ \Leftrightarrow3x=5\Leftrightarrow x=\dfrac{5}{3}\left(tm\right)\)

Bài 2:
a) Ta có: \(\Delta=\left(m-1\right)^2-4\cdot1\cdot\left(-m^2-2\right)\)
\(=m^2-2m+1+4m^2+8\)
\(=5m^2-2m+9>0\forall m\)
Do đó, phương trình luôn có hai nghiệm phân biệt với mọi m
Bài 1:
ĐKXĐ \(2x\ne y\)
Đặt \(\dfrac{1}{2x-y}=a;x+3y=b\)
HPT trở thành
\(\left\{{}\begin{matrix}a+b=\dfrac{3}{2}\\4a-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\4\left(\dfrac{3}{2}-b\right)-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\6-9b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{8}{9}\\a=\dfrac{11}{18}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\dfrac{8}{9}\\2x-y=\dfrac{18}{11}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-\dfrac{18}{11}\\x+3\left(2x-\dfrac{18}{11}\right)=\dfrac{8}{9}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{82}{99}\\y=\dfrac{2}{99}\end{matrix}\right.\)

\(ĐK:x\ne-2\\ PT\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2+2\right)}{x+2}=4\\ \Leftrightarrow\left(x+1\right)\left(x+4\right)=4\left(x+2\right)\\ \Leftrightarrow x^2+5x+4=4x+8\\ \Leftrightarrow x^2+x-4=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1+\sqrt{17}}{2}\\x=\dfrac{-1-\sqrt{17}}{2}\end{matrix}\right.\)

đk: \(x,y\ne-2\)
\(hpt\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x+2}+\dfrac{y}{x+2}=1\\\left(\dfrac{x}{y+2}\right)^2+\left(\dfrac{y}{x+2}\right)^2=1\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}a=\dfrac{x}{y+2}\\b=\dfrac{y}{x+2}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{y+2}+\dfrac{y}{x+2}=1\\\left(\dfrac{x}{y+2}\right)^2+\left(\dfrac{y}{x+2}\right)^2=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\a^2+b^2=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=1-a\\a^2+\left(1-a\right)^2=1\end{matrix}\right.\)
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=0\\b=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}a=1\\b=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=0\\y=2\end{matrix}\right.\end{matrix}\right.\)

Ta có : \(\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}=\dfrac{3}{10}\)
\(\Leftrightarrow\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}=\dfrac{3}{10}\)
\(\Leftrightarrow\dfrac{1}{x}-\dfrac{1}{x+3}=\dfrac{3}{10}\)
\(\Leftrightarrow10\left(x+3\right)-10x=3x\left(x+3\right)\)
\(\Leftrightarrow-3x^2-9x+30=0\)
\(\Delta=\left(-9\right)^2+4.3.30=81+360=441>0\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{9+\sqrt{441}}{-6}=-5\\x_2=\dfrac{9-\sqrt{441}}{-6}=2\end{matrix}\right.\)
Vậy \(S=\left\{-5;2\right\}\)

\(ĐK:x\ne3\\ PT\Leftrightarrow\dfrac{x^2+3x+2}{x-3}\left(-x-1+x^2-2x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{\left(x+1\right)\left(x+2\right)}{x-3}=0\\x^2-3x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\\x=\dfrac{3+\sqrt{41}}{2}\\x=\dfrac{3-\sqrt{41}}{2}\end{matrix}\right.\)

Đk: \(y\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+\dfrac{1}{y}\right)^2-\dfrac{x}{y}=1\\\dfrac{x}{y}-2\left(x+\dfrac{1}{y}\right)=-1\end{matrix}\right.\)
\(\Rightarrow-\left(x+\dfrac{1}{y}\right)^2+\dfrac{x}{y}=\dfrac{x}{y}-2\left(x+\dfrac{1}{y}\right)\)
\(\Leftrightarrow-\left(x+\dfrac{1}{y}\right)^2+2\left(x+\dfrac{1}{y}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{y}=0\\x+\dfrac{1}{y}=2\end{matrix}\right.\)
TH1: \(x+\dfrac{1}{y}=0\Leftrightarrow\dfrac{1}{y}=-x\) thay vào pt dưới ta được:
\(-x^2=-1\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\Rightarrow y=-1\\x=-1\Rightarrow y=1\end{matrix}\right.\)
TH2: \(x+\dfrac{1}{y}=2\Leftrightarrow\dfrac{1}{y}=2-x\) thay vào pt dưới ta được:
\(\left(2-x\right)x-2.2=-1\)\(\Leftrightarrow x^2-2x+3=0\left(vn\right)\)
Vậy (x;y)=(-1;1);(1;-1)
gợi ý \(\left\{{}\begin{matrix}\left(x+\dfrac{1}{y}\right)^2-\dfrac{x}{y}=1\left(1\right)\\\dfrac{x}{y}-2\left(x+\dfrac{1}{y}\right)=-1\left(2\right)\end{matrix}\right.\)
Đem \(\left(1\right)+\left(2\right):\left(x+\dfrac{1}{y}\right)^2-2\left(x+\dfrac{1}{y}\right)=0\)
đến đây chắc bạn có thể tự làm được

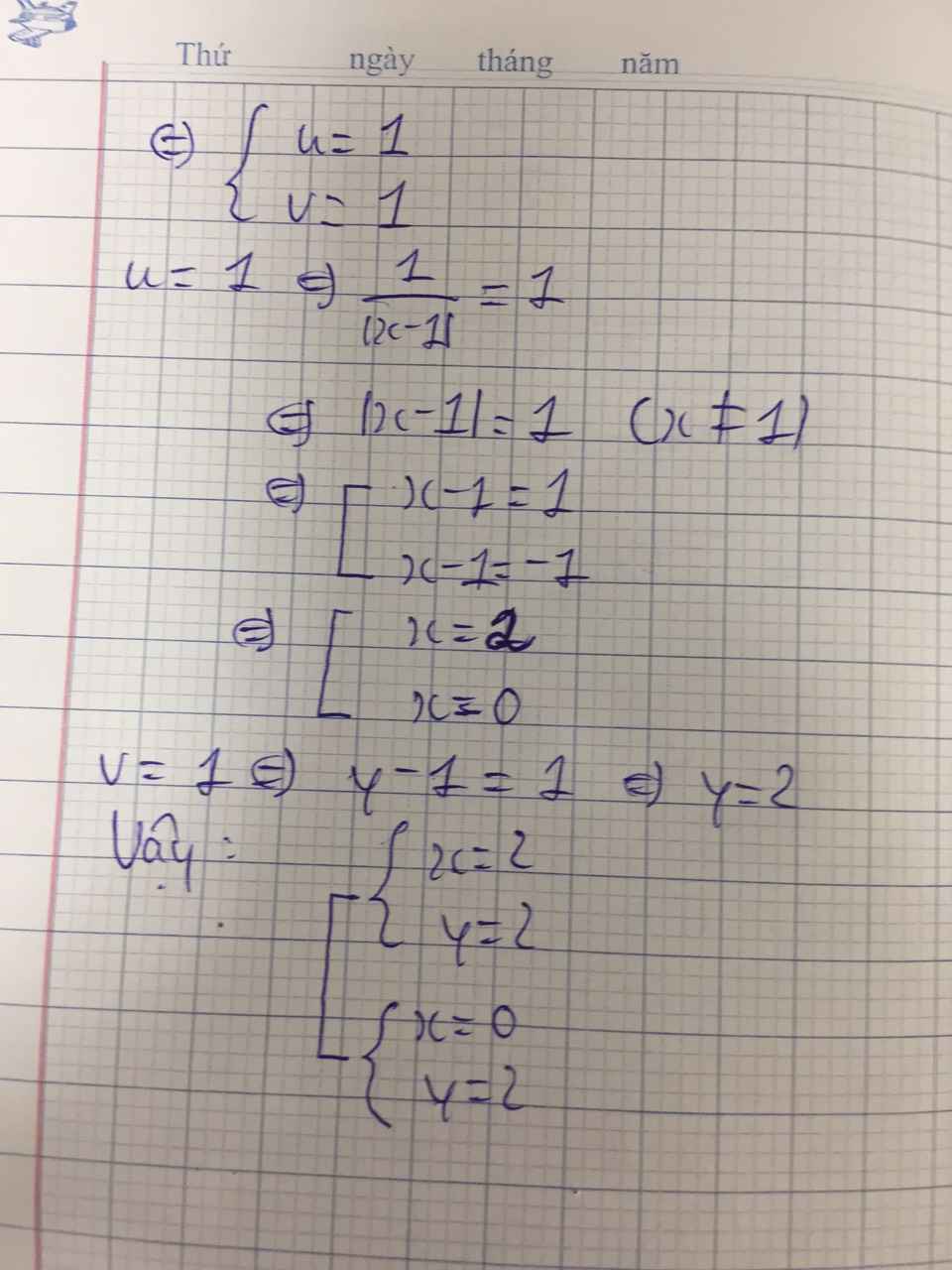
\(ĐK:x\ne0;x\ne1\\ PT\Leftrightarrow\left(\dfrac{1}{x}+2\right)\left(2+\dfrac{x+1}{x-1}-x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{x}=-2\\\dfrac{x+1}{x-1}=x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x+1=x^2-x\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x^2-2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1+\sqrt{2}\\x=1-\sqrt{2}\end{matrix}\right.\)